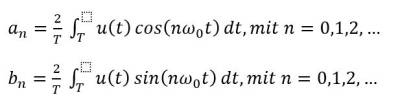Inhaltsverzeichnis
EMV-Labor - Versuchsbeschreibung
Einleitung
Das EMV-Labor ergänzt das Skript zur Vorlesung EMV mit praktischen Übungseinheiten. Das Themengebiet der EMV beheimatet ein Vielzahl verschiedener Disziplinen der Elektrotechnik, von der Netzstabilität bis hin zu elektromagnetischen Wellen im GHz-Bereich. Alle Teilgebiete haben gemeinsam, dass es sich stets um sehr hardwarenahe Themen handelt und sich somit jeder Elektronikentwickler oder Systementwickler früher oder später damit auseinandersetzen muss. Wer die elektromagnetisch Verträglichkeit seiner Produkte verbessern will muss jedoch zuerst in der Lage sein diese auch richtig zu messen bzw. zu bewerten. Damit beschäftigt sich der erste Teil unserer Laborarbeit. Im zweiten Teil nehmen wir einen Tiefsetzsteller in Betrieb, wie er in fast jeder elektronischen Schaltung zur Spannungsversorgung zu finden ist und messen dessen Emissionen. Viel Spaß und Erfolg im Labor!
PS: Bitte lassen Sie sich vom Umfang der Laboranleitung nicht abschrecken. Viele Punkte wiederholen Themen aus dem Studium. Falls Sie mit den einzelnen Punkten vertraut sind können Sie gleich zu den Aufgaben übergehen.
Benötigte Hilfsmittel:
- LTSpice- Installation
- Matlab (Datenauswertung)
Organisation:
Sie können die Versuchsdurchführung überwiegend selbständig gestalten. Nach Rücksprache mit mit Hr. Kletti können Sie auch außerhalb der Vorlesungszeit im Labor arbeiten.
Es findet keine klassische Vorlesung statt. Bitte bereiten Sie sich auf das Labor vor indem Sie die passenden Kapitel zu den Versuchen im Skript bearbeiten. Zu den im LSF angegebenen
Vorlesungszeiten können wir gemeinsam im Labor F222 arbeiten bzw. gebe ich auch allgemeine Hinweise und Einführungen in die Messgeräte sowie Hilfestellung bei den Versuchen.
Die Bearbeitung der Versuche erfolgt üblicherweise in Zweiergruppen.
Dokumentation / Prüfung:
Es ist möglich das Labor auch bereits vor dem Semesterende abzuschließen. Als Dokumentation laden Sie bitte die Ergebnisse der Übungsaufgaben in Moodle hoch. Die Abgabe
eines ausformulierten Berichts ist nicht notwendig. Achten Sie bitte darauf bei Bilddokumentationen oder Grafiken diese in wenigen Sätzen zu interpretieren. Der Prüfbericht zur Komponente
stellt ein eigenes Dokument dar. (Skizzen dürfen generell von Hand gefertigt werden. Es geht nicht um die Form sondern den Inhalt!)
Die Gesamtnote ergibt sich aus der Vollständigkeit Ihrer Dokumente und eine 15 minütige mündliche Prüfung nach Abgabe Ihrer Unterlagen.
Da die Laborplätze leider begrenzt sind, bitte in Moodle anmelden. Moodlekurs EMV (Rebholz)
Teil 1 Rechtecksignale im Zeit- und Frequenzbereich
Rechteckimpulse / Simulation
Rechteckförmige periodische Signale und die Fourierreihe
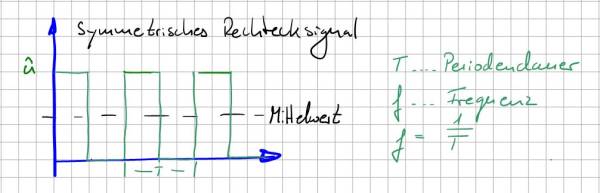
Neben den sinusförmigen Signalen werden in der Elektrotechnik eine Vielzahl an periodischen rechteckförmigen Signale eingesetzt. Die bekanntesten Beispiele sind der Systemtakt von Prozessoren und Mikrocontrollern sowie Taktsignale von leistungselektronischen Systemen zur Leistungssteuerung. Nachfolgende Abbildung zeigt den typischen Verlauf einer symmetrischen periodischen Rechteckfunktion in allgemeiner Darstellung. Die Symmetrie bezieht sich dabei auf das Verhältnis zwischen aktivem und inaktivem Impuls, oder allgemein von Puls- und Pausenzeiten. Sind beide gleich lang, sprechen wir von einer symmetrischen Rechteckfunktion.
Da die Kurve bei 0V startet und die Nulllinie niemals unterschreitet ist sie auf den ersten Blick nicht mittelwertfrei. Mit bloßem Auge ist zu erkennen, dass der eingezeichnete Mittelwert (schwarze Linie im Bild) irgendwo oberhalb der Nulllinie liegt. Der Mittelwert unserer Funktion wird auch Gleichspannungsanteil genannt und lässt sich mit Hilfe der bekannten Gleichung zur Ermittlung des Mittelwerts berechnen (Kurve integrieren und durch die Integrationszeit teilen).
In der EMV-Betrachtung spielt der Gleichanteil mit der Frequenz 0 Hz natürlich keine Rolle. Er ist hier nur vollständigkeitshalber mit aufgenommen. Wichtiger für uns sind die vom Rechtecksignal generierten spektralen Anteile im Frequenzbereich.
Wir wissen: Jedes periodische Signal lässt sich aus einer unendlichen Reihe an Sinus- und Kosinusschwingungen zusammensetzen. Diese Gesetzgebung ist Ihnen sicher unter dem Begriff Fourier-Reihe oder Fourier-Zerlegung bekannt. So zu mindestens die vereinfachte Version. Streng mathematisch müssen noch weitere Bedingungen, wie absolut integrierbar oder eine endliche Anzahl an Maxima und Minima, gegeben sein.
Die symmetrische Rechteckfunktion lässt sich also ausdrücken als:
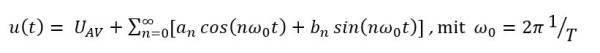 Unser Signal lässt sich also exakt beschreiben aus dem Gleichspannungsanteil zusammen mit einer unendlichen Anzahl an Sinus- und Kosinusschwingungen verschiedener Amplituden a_n und b_n. Schauen wir uns die Argumente der Schwingungen mit cos(nω_0 t) und sin(nω_0 t) genauer an, stellen wir fest, dass diese stets einem Vielfachen der Grundfrequenz entsprechen, als nω_0. Dieser Zusammenhang wird besonders dann wichtig, wenn wir später versuchen den Ursprung einer Rechteckförmigen Störung zu finden. Die Vielfachen Schwingungen der Grundfrequenz werden als Oberschwingungen bezeichnet.
Unser Signal lässt sich also exakt beschreiben aus dem Gleichspannungsanteil zusammen mit einer unendlichen Anzahl an Sinus- und Kosinusschwingungen verschiedener Amplituden a_n und b_n. Schauen wir uns die Argumente der Schwingungen mit cos(nω_0 t) und sin(nω_0 t) genauer an, stellen wir fest, dass diese stets einem Vielfachen der Grundfrequenz entsprechen, als nω_0. Dieser Zusammenhang wird besonders dann wichtig, wenn wir später versuchen den Ursprung einer Rechteckförmigen Störung zu finden. Die Vielfachen Schwingungen der Grundfrequenz werden als Oberschwingungen bezeichnet.
Oberschwingungen treten stets mit einer vielfachen Frequenz der Grundschwingung auf.
In unserem Sprachgebrauch ist die Grundschwingung identisch mit der ersten Oberschwingung (n=1). Oder anders ausgedrückt, die erste Oberschwingung existiert nicht und wir beginnen in der Elektrotechnik bei n=2, der zweiten Oberschwingung. In der Akustik jedoch wird die zweite Oberschwingung als die erste Harmonische bezeichnet, welche ebenfalls die doppelte Frequenz der Grundschwingung besitzt. Bitte bei solchen Angaben immer genau hinterfragen ab wo gezählt wird!
Jetzt aber zurück zu unserer Fourierreihe. Neben den auftretenden Frequenzen interessierten uns vor allem deren Amplituden, welche wir über die Fourier-Koeffizienten an und bn bestimmen.
Bei unserer symmetrischen Rechteckfunktion ist es ausreichend von t=0 bis T/2 zu integrieren, da zwischen T/2 und T die Funktion Null ist. Somit ergibt sich der Koeffizient an zu:
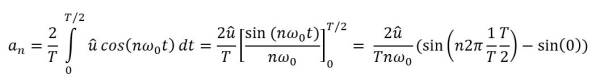 da der Term sin(nπ) unabhängig von n jeweils Null ist, finden wir heraus, dass alle Koeffizienten an=0 sind.
Es verbleiben somit die Koeffizienten bn zu:
da der Term sin(nπ) unabhängig von n jeweils Null ist, finden wir heraus, dass alle Koeffizienten an=0 sind.
Es verbleiben somit die Koeffizienten bn zu:
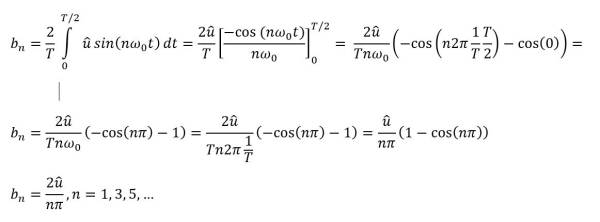
Da die Kosinusfunktion zu -1 wird für alle geradzahligen Werte von n bleiben nur noch die ungeradzahlingen Fourier-Koeffizient bn übrig.
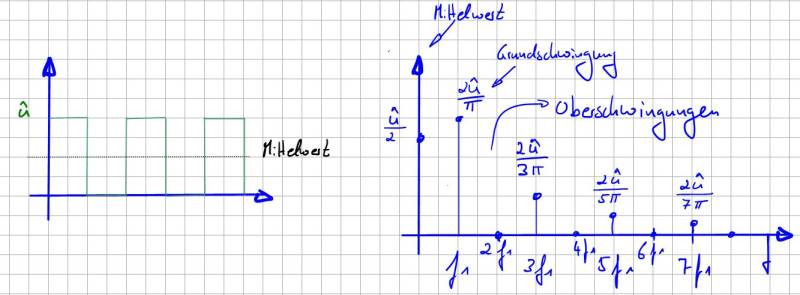
Geschafft, wir sind jetzt in der Lage das exakte Spektrum unseres Rechtecksignals zu berechnen und natürlich auch grafisch darzustellen. Nachfolgende Abbildung zeigt den Übergang des symmetrischen Rechtecksignals vom Zeitbereich in den Frequenzbereich. Schön zu sehen sind die mit 1/x abfallenden Amplituden der Oberschwingungen bei steigender Frequenz.
Die Definition der Fourierreihe hat uns ja bereits gewarnt: „Jedes periodische Signal lässt sich aus einer unendlichen Reihe an Sinus- und Kosinusschwingungen zusammensetzen“. Aber was bedeutet das jetzt für unsere EMV-Eigenschaften? Die Sachlage ist eigentlich eindeutig. Sobald unsere Schaltung ein Rechtecksignal beinhaltet, erzeugen wir damit generell hochfrequente Störgrößen, welche in der Lage sind sich auch außerhalb unserer Anwendung auszubreiten. Der Einsatz von gepulsten Signalen erzwingt somit immer den Einsatz zusätzlicher EMV-Maßnahmen wie Fileschaltungen oder konstruktive Hilfsmittel zur Eingrenzung der hochfrequenten Signale. Da vermutlich die meisten von uns auf dem Schreibtisch kein Spektrumanalysator zusammen mit einem Signalgenerator zur Verfügung haben um sich das Spektrum des Rechtecksignals anzeigen zu lassen, möchte ich ihnen einen anderen Weg zeigen, wie sie schnell ein Gefühl für Spektren verschiedener Zeitbereichssignale bekommen können. Dazu bieten sich Simulationstools wie LT-Spice an, welche zwischenzeitlich nahezu alle mit der Möglichkeit ausgestattet sind, sich zu einem beliebigen Kurvenverlauf das Spektrum berechnen zu lassen.
Einführung in LT-Spice
LT-Spice ist ein klassisches Netzwerksimulationsprogramm. Das bedeutet, im ersten Schritt wird ausgehende vom elektrischen Schaltkreis, eine Netzliste erstellet. In ihr sind die Informationen enthalten welche Bauteile gemeinsame Knotenpunkte besitzen. Im nächsten Schritt werden die Knoten- und Maschengleichungen (Kirchhoffschen Gleichungen) aufgestellt und für jeden Zeitabschnitt gelöst. Das bedeutet, die Simulation berechnet uns sämtliche Spannungen und Ströme im Zeitbereich, analog einer Anzeige am Oszilloskop.
Der Einsatz von Simulationsprogrammen in der Entwicklung elektronischer Schaltungen ist primär dazu gedacht ein vorhandenes Design robuster zu machen durch Parameteranalysen und um die Schaltungen gänzliche in ihrer Funktion zu durchdringen. Leider gibt es für die Programme keinen Plausibilitätscheck. So kann es vorkommen, dass eine falsche Einstellung in der Konfiguration zu schamlos falschen Werten führt. Als Anwender muss man somit alle Ergebnisse hinterfragen und besser noch bereits vor dem Simulationsergebnis eine grobe Idee davon haben wie das Ergebnis wohl aussehen wird. Falls man dann doch mal vom Ergebnis überrascht wird würde ich dringend empfehlen zahlreiche Plausibilitätsprüfungen durchzuführen (Vereinfachungen und Abschätzungen). Daher ist es generell sinnvoll mit jedem neuen Tool analytisch bekannte Strukturen und Vorgänge zur Verifikation heranzuziehen.
Spice steht für „Simulation Program with integrated Circuit Emphasis“ und wird auch als Berkeley-Spice bezeichnet, als Hinweis auf dessen Anfänge an der Berkeley University of Carlifornia. Heutzutage sind zahlreiche Derivate verfügbar, die sich meist in ihrer Oberfläche und Handhabung unterscheiden. Die vom Halbleiterhersteller Analog Devices (vormals Linear Technolgogies) entwickelte Version als LT-Spice überzeugt durch eine sehr benutzerfreundliche Oberfläche und einfache Bedienbarkeit. Das Programm ist über die Homepage von Analog Devices (analog.com) kostenlos beziehbar.
Für die Einführung in LT-Spice und als erste Übung möchte ich den zuvor besprochenen Rechteckimpuls im Zeit- und Frequenzbereich in einer Simulation verifizieren. Eine umfängliche Einführung in LT-Spice würde den Umfang dieses Buches sicher sprenge womit ich auf die zahlreichen Youtube-Videos und Onlineliteratur verweise möchte. Wir schauen uns aber die wichtigsten Einstellungen im Folgenden gemeinsam an.
Das symmetrische Rechtecksignal wird generiert über eine allgemeine Spannungsquelle (voltage) welche wir im ersten Schritt in der Bauteilbibliothek auswählen, siehe Abbildung Schritt 1.
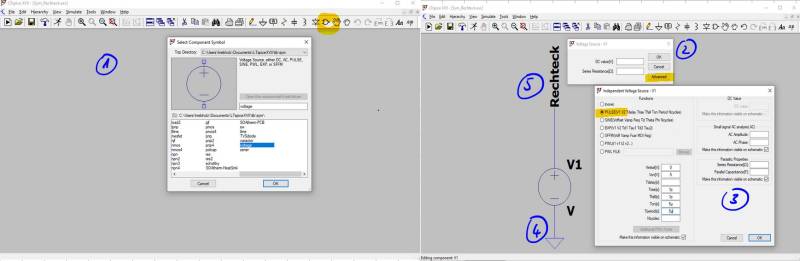 Die Spanungsquellen in LT-Spice können beliebig, vom reinen DC bis hin zur Puls-Quelle, konfiguriert werden. Es ist sogar möglich, den Spannungsverlauf aus einer externen Quelle, zum Beispiel einem Excel-Sheet, zu importieren. Standartmäßig geht das Programm davon aus, dass wir einfache DC-Quellen verwenden möchten, zusammen mit einem Innenwiderstand der Quelle. Wählen Sie in Schritt zwei den Punkt Advanced um unsere Pulsquelle Pulse im dritten Schritt zu spezifizieren. Generell rate ich davon ab in einem Untermenü einen Quellwiderstand Series Resistance zu setzten. Falls es notwendig ist einer Spannungs- oder Stromquelle einen Innenwiderstand zuzuweisen ist es am übersichtlichsten dies direkt im Schaltplan als diskretes Bauteil zu machen. Versteckte Widerstände werden später gerne bei der Auswertung oder der Fehlersuche vergessen!
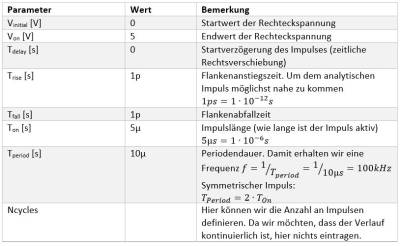
Folgende Tabelle zeigt die zur Nachbildung des Impulses notwendigen Einstellungen:
Die Spanungsquellen in LT-Spice können beliebig, vom reinen DC bis hin zur Puls-Quelle, konfiguriert werden. Es ist sogar möglich, den Spannungsverlauf aus einer externen Quelle, zum Beispiel einem Excel-Sheet, zu importieren. Standartmäßig geht das Programm davon aus, dass wir einfache DC-Quellen verwenden möchten, zusammen mit einem Innenwiderstand der Quelle. Wählen Sie in Schritt zwei den Punkt Advanced um unsere Pulsquelle Pulse im dritten Schritt zu spezifizieren. Generell rate ich davon ab in einem Untermenü einen Quellwiderstand Series Resistance zu setzten. Falls es notwendig ist einer Spannungs- oder Stromquelle einen Innenwiderstand zuzuweisen ist es am übersichtlichsten dies direkt im Schaltplan als diskretes Bauteil zu machen. Versteckte Widerstände werden später gerne bei der Auswertung oder der Fehlersuche vergessen!
Folgende Tabelle zeigt die zur Nachbildung des Impulses notwendigen Einstellungen:
Mit den Einstellungen für die Spannungsquelle haben wir uns ein symmetrisches Rechtecksignal konfiguriert, welches einem idealen Impuls möglichst nahekommt. Da keiner der Spice-Löser in der Lage ist geschlossene analytische Lösungen zu berechnen, sondern sich dem Ergebnis iterativ annähert, müssen wir mit geringen Abweichungen zum Formelergebnis rechnen. Die größten Fehlerquellen in unserem Beispiel stellen die Flanken des Impulses bzw. die An- und Abfallzeiten dar, welche in der Berechnung nicht berücksichtigt wurden.
In Schritt 4 müssen wir der noch einfachen Schaltung einen Referenzknoten zuweisen, auf den alle Berechnungen und später dann auch das Ergebnis der Knotenspannungen bezogen werden. Alle Simulationsprogramme bezeichnen diesen Punkt als (Spice) Null-Knoten. Sie finden das Symbol in der oberen Menüleiste. In unserer realen Schaltung entspricht dieser Punkt der Masse bzw. dem Rückleiter. Neben dem Symbol der Referenzmasse befindet sich das Werkzeug zur Erstellung von Leitungsverbindungen. Damit kann der negative Anschluss der Spannungsquelle mit dem Massepunkt verbunden werden.
Ihre Schaltung sieht nun schon fast so aus wie mein Setup im gezeigten Beispiel. Zur übersichtlicheren Darstellung können wir zum Abschluss in Punkt 5 noch ein beliebiges Label für das an der Impulsquelle angeschlossene Netz vergeben. Verwenden Sie dazu den Befehl Label Net.
Die Konfiguration ist nur bereit zur Simulation. Wir müssen dem Algorithmus nur noch mitteilen welche Art von Informationen er für uns berechnen soll. LTSpice bietet verschiedene Analysemethoden elektrischer Schaltungen an. Die wichtigste Simulationsart stellt die sogenannte Transientanalyse dar, welche die Schaltung in definierten Zeitschritten berechnet. Je kleiner die Zeitschritte, desto länger dauert verständlicherweise die Simulation. Starten Sie jetzt bitte die Simulation mit dem Befehl Run.
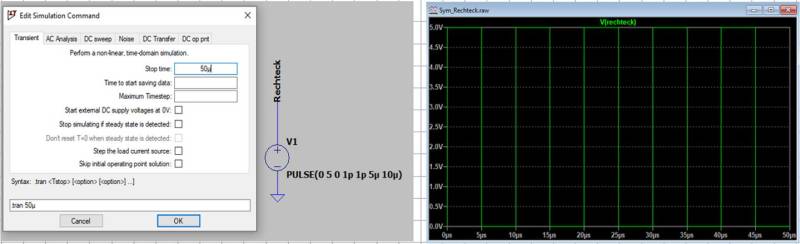
Das Programm erkennt, dass noch keine Simulationsart ausgewählt wurde und zwingt uns nun die Simulationsparameter anzugeben. Standardmäßig wird die Transientanalyse vorgeschlagen bei der wir lediglich die gewünschte Simulationsdauer angeben müssen. Nach erfolgreicher Simulation wird der Mauszeiger zu einer Messspitze, mit der sich Spannungen mit Bezug zur Referenzmasse anzeigen lassen.
Zur Anzeige eines Rechteckimpuls im Zeitbereich bedarf es sicher keiner Simulation. Unser Interesse gilt eh den im Signal enthaltenen hochfrequenten Anteilen. Das bedeutet wir müssen jetzt in den Frequenzbereich wechseln. Bei aktivem Ergebnisplot gelangt man unter View → FFT in das Menü zur Spezifikation der Frequenzanalyse. FFT steht für die Fast Fourier Transformation, welche in der Lage ist, die Frequenzanteile eines digitalisierten Signals zu berechnen. Für unser einfaches Beispiel können wir die Standardeinstellungen übernehmen und erhalten folgendes Ergebnis:
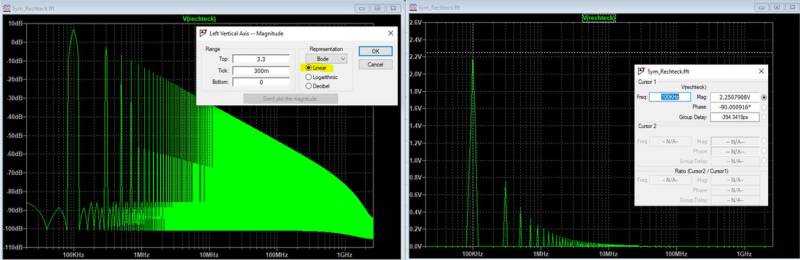
Da wir uns mit logarithmischen Größenordnungen erst im nächsten Abschnitt befassen, bitte zuerst mit einem Rechtsklick auf die Y-Achse die Beschriftung in Linear umstellen.
Geschafft, wir sehen nun (rechts) die im Rechtecksignal enthaltenen Frequenzanteile in der Einheit Volt [V]. Mit Hilfe der Cursorfunktion lassen sich jetzt komfortabel die Amplituden und die Phasenlage an diskreten Frequenzpunkten bestimmen. Die Auflösung auf der Frequenzachse ist mit 20kHz noch sehr grob, für unsere Zwecke allerdings mehr als ausreichend. Denn wir wissen ja, dass sämtliche Oberschwingungen einem ganzzahligen Vielfachen der Grundschwingung (100kHz) entsprechen. Die Frequenzauflösung lässt sich problemlos erhöhen, indem die Simulationszeit im Zeitbereich erhöht wird, z.B auf 100µs oder 1ms.
Bei genauerer Betrachtung der Frequenzachse stellen wir fest, dass wie erwartet die geradzahligen Vielfachen der Grundfrequenz nicht existieren. Somit verbleiben lediglich die ungeradzahligen Oberschwingungen welche sich über die Gleichung bn=(2∙5V)/nπ berechnen lassen.
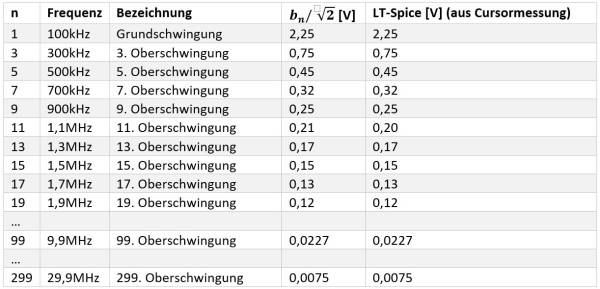
Bevor wir die Daten aus der Rechnung und Simulation miteinander vergleichen können müssen wir die Fourierkoeffizienten in die Effektivwerte umrechnen über den Faktor 1/√2. Leider gibt es keine Regel, ob ein Messgerät oder Simulationsprogramm die Effektiv- oder Spitzenwerte anzeigt. Oft haben sich die Hersteller für die Effektivwerte entschieden. Selbst die Hilfefunktion von LTSpice lässt diese Frage unbeantwortet. In vielen kann diese Frage mit einem einfachen Test beantwortet werden. Dazu lässt man sich den Fourierkoeffizienten einer Sinusfunktion berechnen mit bekannter Amplitude. Ist dieser identisch, wie die im Zeitbereich eingestellte Amplitude handelt es sich um den angezeigten Spitzenwert. Ist dieser um den Faktor 1/√2 kleiner, den Effektivwert. Die dargestellte Tabelle vergleicht die berechneten Fourierkoeffizienten mit den aus der Simulation angezeigten Daten. Beide Spalten zeigen wie erwartet dieselben Ergebnisse womit wir davon ausgehen können, dass wir die Rechnung fehlerfrei durchgeführt haben. Die große Stärke einer Simulation zeigt sich allerdings erst wenn wir uns Signale anschauen deren Fourierkoeffizienten nicht so einfach zu berechnen sind wie im zuvor gezeigten Beispiel.
Aufgabe 1
Erstellen Sie ihre eigene LTSpice Simulation eines Rechteckimpuls und beobachten Sie wie sich das Spektrum ändert bei:
- a) einer Verdoppelung und Verdreifachung der Simulationsdauer
- b) einem unsymmetrischen Rechtecksignal
- c) einem trapezförmigen Impuls mit An- und Abfallzeiten
Schalten Sie dabei bitte jeweils die Anzeige im Frequenzbereich um zwischen linearer und logarithmischer Darstellung in dB. Was fällt ihnen dabei auf?
Pegelmaße
Sicher ist Ihnen bereits aufgefallen, dass Messgrößen und Grenzwerte in der EMV häufig in dB ausgedrückt werden. Selbst LTSpice zeigt im Frequenzbereich bevorzugt das Ergebnis als Pegelmaß in dB an. Vermutlich haben Sie bereits selbst herausgefunden, dass die lineare Anzeige unserer Fourierkoeffizienten im Frequenzbereich für höhere Frequenzen bald an ihre Grenzen stößt. Nur umständliches heranzoomen erlaubt es uns den exakten Wert zu ermitteln. Ganz anders in der logarithmischen Darstellung, oder wenn wir das Ergebnis in dB betrachten. Die Werte sind über den gesamten Frequenzbereich darstellbar. Genau darin liegt die Stärke der in der EMV gebräuchlichen Darstellung in dB. Die Einheit dB ist ein Kunstwort, das sich zusammensetzt aus dem Buchstaben „d“ für Dezi, welches für die Multiplikation mit dem Faktor 10 steht, sowie dem Buchstabe B welcher zu Ehren des Alexander Graham Bell (1847 – 1922) geführt wird. Bell war maßgeblich an der Industrialisierung der Telefonie beteiligt und kommerzialisierte den Telefonapparat. In Wirklichkeit handelt es sich bei der Bezeichnung db um keine „richtige“ Einheit, vergleichbar wie U oder I für Spannungen und Ströme. Wikipedia spricht sogar von einem Pseudomaß! Das liegt daran, dass der es sich eher um eine Darstellungsform handelt, welche auf dem Logarithmus zur Basis 10, also (log)10 basiert. Und hier liegt auch schon das Geheimnis der Pseudoeinheit. Genauso wenig wie es möglich ist den sin(5V) zu bilden ist es ebenfalls nicht möglich den Logarithmus log(10A) zu bilden. Beide Funktionen erwarten einheitslose Argumente! Um die Einheiten loszuwerden müssen wir uns auf eine Referenz beziehen, welche beliebig gewählt werden darf. Damit auch unser Bürokollege weiß was bei einer Umrechnung gemeint ist wird am Ende der dB Angabe die Bezugseinheit gesetzt.
Beispiel: Bei der Umrechnung von 5V in dB kommt der Ausdruck log(5V/1V) zum Einsatz. Der Referenzwert oder auch Bezugsgröße um die Einheiten herauszukürzen beträgt also 1V, womit das Ergebnis dann in dBV ausgedrückt wird. Achtung, hier ist noch nicht die vollständige Formel dargestellt, welche erst im nächsten Abschnitt vorgestellt wird. Nachfolgende Tabelle zeigt einige Beispiele von Bezugsgrößen und die daraus resultierende Bezeichnung.

In der Fachwelt hat sich vermutlich aus Faulheit für die Darstellung von Leistungspegeln, mit dem Bezugspegel 1mW, eine Anomalie eingeschlichen. So ist es üblich den Pegel nicht als dBmW anzugeben, sondern nur als dBm. Simulationsprogramme wie LTSpice oder auch Oszilloskope mit implementierter FFT Funktion verzichten teilweise komplett auf weitere Angaben und haben jeweils feste Bezugsgrößen von 1V. Sämtliche Angaben, ob Strom oder Spannungswerte werden dementsprechend nur als dB gekennzeichnet. Wird also in diesen Systemen ein Spannungswert in dB dargestellt wissen wir es handelt sich in Wirklichkeit um die Angabe dBV, bei einem Stromwert um die Angabe dBI. Wie bereits im vorhergehenden Beispiel, zur Frage ob Spitzen- oder Effektivwerte angezeigt werden, kann ein einfache Simulation mit bekanntem Ergebnis herausfinden in welcher Form die Pegelmaße wiedergegeben werden.
Nachfolgende Tabelle zeigt einige Beispiele zur Umrechnung linearer Größen in dB Pegelmaße für gängige Einheiten in der EMV. Die Liste ist beliebig erweiterbar. Es ändert sich lediglich jeweils die Bezugsgröße.

Leider gibt es auch bei der Umrechnung kein einheitliches System. Die Ursache findet sich im quadratischen Zusammenhang der Leistung an einem reellen Widerstand, mit P=U2/R=I2∙R. Aus den Rechenregeln des Logarithmus wird das Quadrat im Argument zu einer Multiplikation und damit aus 10 log(…2 )=2∙10 log(…)=20 log(…). Am einfachsten man merkt sich den Faktor 10 für die Leistungspegel als Alleinstellungsmerkmal. Alle weiteren Pegelmaße für Spannungen, Ströme, Feldstärken usw. werden mit dem Faktor 20 berechnet.
Pegelmaße und Kopfrechnen
Auch wenn es auf den ersten Blick merkwürdig erscheinen mag, aber für die gängigsten Alltagsaufgaben in der EMV lassen sich Pegelmaße sehr einfach ohne Taschenrechner berechnen oder mindestens abschätzen. Unser wichtigster Punkt ist der Logarithmus von Eins, welcher Null ergibt, log(1)=0. Wir erinnern uns an Mathe, dass der Logarithmus von Null nicht definiert ist! Das bedeutet wir sind in der Lage mit Pegelmaßen sehr kleine Größen darzustellen, aber halt keine Null.
Mit diesen sehr einfachen Regeln können wir ohne Nachdenken folgende Pegelmaße bestimmen:
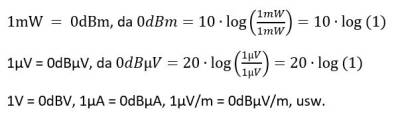
Die Rechnung wird nur geringfügig komplizierter, falls der umzuwandelnde Wert einer Zehnerpotenz der Bezugsgröße entspricht. Wir wissen log(10) = 1, log(100) = 2, log(1000) = 3 usw.. Folgende Beispiele zeigen den Zusammenhang am Beispiel der Umrechnung von µV in dBµV:
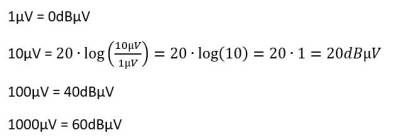
Vorsicht ist geboten bei der Berechnung von Leistungspegeln, da hier mit dem Faktor 10 vor dem Logarithmus gearbeitet wird:

Die Zwischengrößen lassen sich ohne Taschenrechner nicht ohne Weiteres berechnen. Allerdings kann in vielen Fällen eine Abschätzung für eine Verdoppelung des linearen Wertes herangezogen werden.
+3dB entspricht näherungsweise einer Verdoppelung der Leistung
+6dB entspricht näherungsweise einer Verdoppelung der Spannung, Strom, ….
Bei jeder Verdoppelung stimmt unsere Abschätzung bis auf die erste Nachkommastelle mit dem berechneten Wert überein. Damit ist unsere Überschlagsrechnung für die meisten Anwendungsfälle ausreichend genau.
Das Prinzip funktioniert natürlich auch Rückwärts. Als Beispiel schauen wir uns noch einmal das Frequenzspektrum unseres Rechteckimpuls an, allerdings jetzt in dB Darstellung.
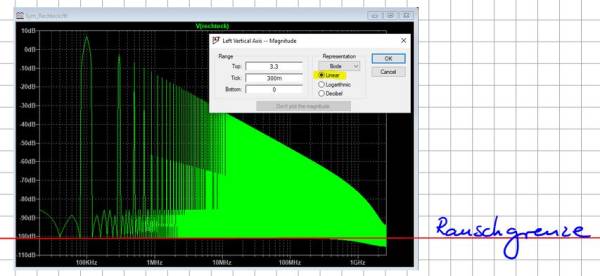
Wir schauen jetzt aber nicht auf die Amplituden der Oberschwingungen, sondern auf das was nicht da ist?! Grob abgeschätzt gibt uns LTSpice als kleinsten berechneten Wert ca. -100dB an. Doch welchem Spannungswert entspricht dieser Pegel? Wendet man die Rechenregeln rückwärts an erfolgt im ersten Schritt die Division des Pegelwerts durch den Divisor 20, also
(-100dB)/20=-5
Somit wissen wir, dass der gesuchte Spannungswert um den Faktor 100.000 kleiner ist als die in LTSpice verwendete Bezugsgröße von 1V, also 1/100.000 V oder 10µV. Dieser kleinste angezeigte Wert ist in der EMV eine wichtige Größe, welche oft als die Rauschgrenze bezeichnet wird. Im Fall unserer Simulation könnte man sagen, es handelt sich um numerisches Rauschen.
Der Wert ist deshalb so wichtig, da wir jetzt wissen, dass unser Messgerät oder die Simulation nicht in der Lage ist Werte auszugeben, welche unterhalb dieser Grenze liegen. Theoretisch könnten sich Oberschwingungen unterhalb dieser Rauschgrenze verstecken. Um diese zu finden müssten wir ein genaueres Messgerät zu rateziehen oder die Simulationseinstellungen anpassen. Die Abbildung zeigt die Rauschgrenze unserer Simulation mit einem Wert von ca. 10µV. Wie wir bei den Messungen später sehen werden ist es wichtig die aktuellen Rauschgrenzen zu ermitteln, bevor mit der eigentlichen Messung begonnen wird. Nur so kann herausgefunden werden ob die Störung vom Prüfling kommt oder das Messgerät eigene bzw. externe Störungen erfasst.
Aufgabe 2
Berechnen Sie folgende Pegelmaße ohne Taschenrechner:
- a) 10V in dBµV
- b) 1mV in dBµV
- c) 3mV in dBµV
- d) 20W in dBm
- e) 50W in dBm
- f) 1kW in dBm
Berechnen Sie folgende Pegelmaße in lineare Größen
- g) 100dBV in V
- h) 126dBµV in V
- i) 132dBµV in V
Aufgabe 3
Der Grenzwert für leitungsgebundene Emissionen (Störspannungsmessung nach DIN EN 61000-6-3, leitungsgebundene Störemissionen) beträgt bei 500kHz 46dBµV.
Welche maximale Spannungsamplitude darf ein symmetrisches Rechtecksignal mit der Grundfrequenz von 100kHz maximal besitzen, damit der Grenzwert nicht überschritten wird?
Transiente Störgrößen
Jeder kennt das typische Knacken im Radio und die Störungen im TV während eines Gewitters. Das bedeutet, dass auch kurze, einmalig auftretende Impulse elektromagnetische Signale emittieren die sich ausbreiten können. Bei dieser Art von Impulsen sprechen wir auch von transienten Störungen (engl. VFT Very Fast Transient). Da die Störungen im Rundfunkempfang unabhängig sind vom aktuell gehörten Sender lässt sich bereits erahnen, dass diese Art von Impulsen eine Vielzahl unterschiedlicher Frequenzen emittieren. Wir werden im Verlauf dieses Kapitels sehen, dass nicht nur diskrete Frequenzanteile emittiert werden, sondern alle Frequenzen. Wir sprechen dann von einem sogenannten breitbandigen Spektrum. Neben den bekannten Blitzentladungen erzeugen ESD-Impulse oder einmalige Schalthandlungen breitbandige transiente Signale.
Zur mathematischen Beschreibung dieser Signale beobachten wir was in unserer Simulation des Rechteckimpuls passiert, wenn wir die Periodendauer bei gleichbleibender Impulsbreite stetig erhöhen. Dadurch wird aus unserem periodischen Signal langsam ein einmalig auftretender transienter Impuls.
Lassen Sie uns dazu erneut einen 5µs langen Impuls mit einer Amplitude von 5V betrachten. Mit LTSpice lässt sich sehr komfortabel ein Parametersweep durchzuführen. Dabei wird die Schaltung für verschiedene Werte nacheinander simuliert und das Ergebnis dargestellt. Die Aufforderung die Simulation mehrfach zu durchlaufen findet sich in der Anweisung (Spice Directive) „.step param Period list 10µ 100µ 10m“. Period wird ab jetzt als Variable behandelt und muss in bei der weiteren Verwendung in geschweifte Klammern gesetzt werden.

Mit dem Setup erzeugen wir uns ein Rechteckimpuls mit 5V Amplitude, einer Impulsdauer von 5µs, Anstiegs- und Abfallzeit von 100ns und einer variablen Periodendauer {Period}. Das Simulationsergebnis im Zeitbereich ist eine reine Visualisierung und hält keine Überraschungen bereit. Viel interessanter ist die Darstellung der Signale im Frequenzbereich. Deutlich zu sehen ist, dass je größer die Periodendauer gewählt wird, desto mehr Spektrallinien vorhanden sind (Vergleiche dazu die Anzahl an auftretenden Oberschwingungen der Blauen und Grünen Kurve in nachfolgender Abbildung). Bei einer Periodendauer von 1ms sind sogar gar keine einzelnen Oberschwingungen mehr zu erkennen. LTSpice berechnet uns eine durchgezogene Linie, was bedeutet, in diesem Bereich sind alle möglichen Frequenzen enthalten.
Genau jetzt sind wir an unserer ursprünglichen Definition von breitbandigen Signalen angekommen. Sie erinnern sich, dass unser Radiosignal gestört wird, unabhängig vom eingestellten Sender. Dieser Umstand ist es auch warum transienten Impulsen in der EMV von besonderer Bedeutung sind. Die Wahrscheinlichkeit, dass der transiente Impuls eine Frequenz enthält auf die ein System vielleicht empfindlich reagiert liegt somit bei 100%. Bei periodischen Störungen ist es eher unwahrscheinlich, dass eine harmonische der Grundfrequenz exakt auf einer Empfangsfrequenz liegt. In modernen Kraftfahrzeugen werden kritischen Komponenten, welche häufig den Radioempfang stören, die aktuell vom Kunden eingestellte Frequenz über den CAN-Bus mitgeteilt. Das entsprechende Steuergerät legt die Taktfrequenz dann so, dass dessen Harmonischen möglichst weit weg sind vom Trägersignal des Kommunikationskanal.
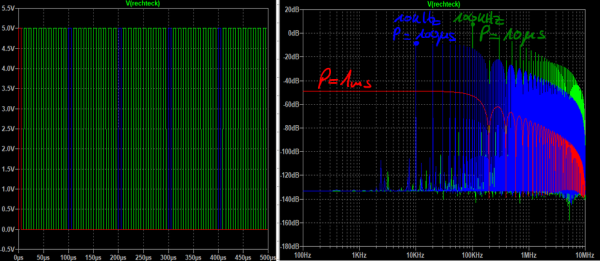
Je länger die Periodendauer gewählt wird, das bedeutet je singulärer der Impuls wird, desto geringer wird die Amplitude des kontinuierlichen Frequenzspektrums. Physikalisch lässt sich das dadurch erklären, dass sich die Signalenergie jetzt auf viel mehr Frequenzanteile verteilen muss, als bei den Signalen mit geringerer Periodendauer. Ich will nicht verschweigen, dass LTSpice in Wahrheit gar nicht in der Lage ist das Frequenzspektrum einmalig auftretender Impulse zu berechnen. Der zugrundeliegende FFT (Fast Fourier Transform) Algorithmus setzt die im Zeitbereich berechneten Daten einfach periodisch fort. Somit erzwingt LTSpice eine künstliche Periodizität beim Übergang in den Frequenzbereich. Durch eine entsprechend lange gewählte Simulationsdauer von 10ms im Vergleich zur Impulsdauer lässt sich der Übergang zu einem kontinuierlichen Spektrum dennoch gut darstellen.
Transiente Störungen lassen sich im Frequenzbereich als breitbandiges Signal beschreiben.
Breitbandige Signale enthalten, abgesehen von wenigen Nullstellen, sämtliche Frequenzanteile.
Mathematisch lassen sich singuläre Vorgänge mit Hilfe des Fourier-Integral in den Frequenzbereich übertragen. Die Berechnung beinhaltet jetzt keine Grundfrequenz mehr bzw. Vielfache der Grundfrequenz nω0 wie bei der Fourier-Reihe. Vielmehr wird ein kontinuierliches Spektrum berechnet.
Das Fourier-Integral
Das kontinuierliche Spektrum eines einmaligen Impulses lässt sich mit Hilfe der Integration des Impulses im Zeitbereich berechnen zu:
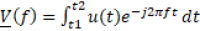
V(f) wird dabei als Spektralfunktion oder Spektraldichte bezeichnet. Mit ihr lassen sich transiente Impulse im Frequenzbereich bewerten und gegenüberstellen. Auch hier gilt natürlich, je größer die Amplitude der Sprektraldichte, desto größer ist dessen Störpotential.
Für unsere tägliche Arbeit im Labor ist diese Art der Impulsbeschreibung allerdings wenig hilfreich. Es gibt schlichtweg keine Messgeräte die in der Lage sind die Spektraldichte eines singulären Impulses aufzuzeichnen. Selbst wenn wir mit dem Oszilloskop den Impuls im Zeitbereich einfangen, erfolgt bei der Anwendung des FFT-Algorithmus bei der Auswertung mit Matlab die zuvor in LTSpice beschriebene periodische Fortsetzung des Zeitsignals. Das bedeutet aber auch, dass wenn im Zeitbereich gemessene Beispiel Blitz- oder ESD-Entladungen mit einander verglichen werden sollen die Zeitbasis der Zeitaufzeichnung identisch sein muss. Andernfalls sind die Amplituden nach einem Übergang in den Frequenzbereich nur noch bedingt miteinander vergleichbar.
Im Gegensatz zum Spektrum eines periodischen Signals hat die Spektraldichte übrigens eine andere Dimension, nämlich Spannung mal Zeit [Vs]. Das wird deutlich, wenn wir das Fourierintegral für f = 0 betrachtet:
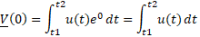
Die Lösung für V (0) ist demnach stets reell und entspricht dem Flächeninhalt unter der Kurve in Vs (Voltsekunden). Die Frage stellt sich natürlich warum das Fourier-Integral hier vorgestellt wird, obwohl es auf den ersten Blick zu nichts Praktischem zu gebrauchen ist. Berechtigt!
Das ändert sich, wenn wir einen realen singulären Rechteckimpuls im Zeitbereich betrachten. Dieser lässt sich beschreiben über seine Flanken An- und Abfallzeit sowie einen idealen Rechteckimpuls. Damit erhält man einen Trapezimpuls, auf welchen das Fourier-Integral anwendbar ist. Tp ist, im Unterschied zur bekannten Beschriftung von Reckteckgrößen ohne die Impulsflanken, hier die mittlere Impulsdauer, bei der jeweils die halbe Anstiegszeit τ berücksichtigt wird. ̂u entspricht dem Spitzenwert des Trapezimpuls.
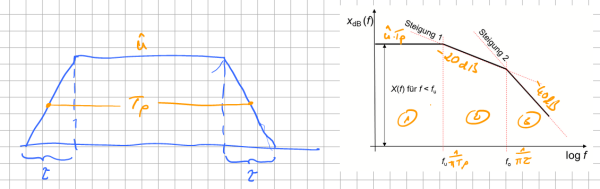
Das Ergebnis des Fourier-Integral zum idealen Rechteckimpuls ist in obiger Abbildung dargestellt. Da wir stets die maximale Störemission suchen, ist es ausreichend das Ergebnis so zu vereinfachen, dass nur noch die Hüllkurve der Spektraldichte betrachtet wird. Dieser Verlauf der Hüllkurve lässt sich in drei Bereiche einteilen.
- Die Amplituden der auftretenden Frequenzanteile sind bis zur Frequenz fu konstant und bestimmen sich zu u*Tp, also die Spannungszeitfläche. Für den Effektivwert der auftretenden Spannung im Frequenzbereich muss der Wert mit √2 dividiert werden.
- Ab der Frequenz fu sinken die Amplituden der Spektraldichte mit 1⁄f. In logarithmischer Darstellung entspricht diese Reduktion einem Abfall von -20dB/Dekade (sprich 20 dB pro Dekade). Das bedeutet, eine Störamplitude welche zum Beispiel bei 1kHz dem Wert 60dBµV entspricht ist bei einer Dekade weiter, als 10kHz, auf 40dBµV abgesunken. Dieser Zusammenhang gilt immer, unabhängig der gewählten Einheit (dBV, dBµV, dBI, …). Die Frequenz fu berechnet sich zu fu=1/(πT_p ).
- Ab der Frequenz fo geht es steil bergab mit den Störgrößen bzw. den Amplituden der Amplitudendichtefunktion. Diese sinkt nun mit 1⁄f^2 welches einem Abfall von -40dB/Dekade entspricht. Die erste Eckfrequenz fu ist von Seiten der EMV nur selten beinflussbar, da die Impulslänge aufgrund funktionaler Gesichtspunkte festgelegt wird. Auf die Flankenanstiegs hingegen kann in vielen Fällen in Grenzen Einfluss genommen werden. Besonders unter dem Hinweis, dass sich die Frequenz fo berechnet zu fo=1/πτ. Daraus wird sofort ersichtlich, je kleiner die Flankenanstiegszeit, desto geringer fallen die hochfrequenten Anteile aus.
EMV-Tafel
Das Fourier-Integral findet häufige Anwendung in der sogenannten „EMV-Tafel“. Wie bereits beschrieben macht es meist keinen Sinn das Frequenzspektrum eines singulären Impulses auszuwerten. Hier ist die absolute Amplitude interessanter, da sie wie im Fall eines Blitz- oder ESD-Impuls über den Zerstörungsgrad bei einer Beaufschlagung entscheidet. Periodische Störimpulse treffen wir jedoch sehr häufig an, sei es bei der Pulsweitenmodulation, bei Kommunikationssignalen oder allgemein bei Taktsignalen. Oft suchen wir als EMV-Ingenieur in detektivischer Kleinarbeit welche Schaltungseinheit die Störungen emittiert oder wir möchten im Vorfeld die auftretenden Störgrößen vorhersagen. Ein Hilfsmittel mit dieser Funktionalität findet sich in der EMV-Tafel!
Das Ergebnis der Fourier-Integration, die Spektraldichte, lässt sich auf einfache Weise erweitern zu ein Frequenzspektrum für periodische Signale. Um den Spitzenwert der der Amplituden im Frequenzbereich bis zur Eckfrequenz fu zu erhalten muss das Ergebnis aus dem Spektrum lediglich mit der Wiederholfrequenz f des periodischen Impuls multipliziert werden.

Das Spektrum des periodischen Signals zeigt dann natürlich nicht mehr die Eigenschaften eines breitbandigen Impulses, sondern enthält die bekannten Nullstellen und Maxima periodischer Rechtecksignale. Die beiden Eckfrequenzen fu und fo bleiben erhalten. Dadurch lassen sich aus der Impulsdauer und Flankenanstiegszeit direkt Rückschlüsse über das auftretende Störspektrum machen. Folgende Zusammenhänge können dabei generell festgestellt werden:
- Je länger die Impulsdauer Tp (bei konstanter Periodendauer), desto größer sind die Amplituden des Spektrums bis zur ersten Eckfrequenz fu.
- Je länger die Impulsdauer Tp, desto früher wird die erste Eckfrequenz fu erreicht womit das Spektrum bei steigender Frequenz mit 20dB/Dekade abfällt.
- Je größer die Flankenanstiegszeit τ, desto früher wird die zweite Eckfrequenz fo erreicht womit das Spektrum bei steigender Frequenz mit 40dB/Dekade abfällt
In der praktischen Umsetzung ist die Impulsdauer meist fest an die Funktionalität der Schaltung gekoppelt. Unser größter Stellhebel liegt demnach in einer Reduktion der Flankenanstiegszeit bzw. Abfallzeit τ. Dieser Trick wird meist für Kommunikationsleitungen und leistungselektronische Schaltungen mit sogenannten hart schaltenden Leistungshalbleitern angewendet. Schauen wir uns jetzt ein konkretes Beispiel eines Rechteckimpuls mit folgenden Parametern an:
| Parameter | Wert |
|---|---|
| Amplitude / Spitzenwert | V |
| Impulsdauer | 3µs |
| An-/Abfallzeit (Flanke) | 40ns |
| Mittlere Impulsdauer | 3µs+ 40ns = 3,04µs |
| Frequenz / Periodendauer | 10kHz,T=100µs |
Nachfolgende Abbildung zeigt die Simulation des Rechteckimpuls im Zeitbereich und die notwendigen Simulationseinstellungen für eine Spannungsquelle, konfiguriert als Impulsquelle.
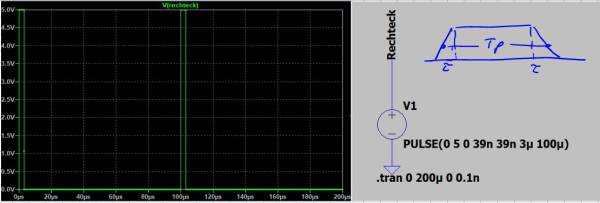
Der Spitzenwert uFB der Amplituden im Frequenzbereich bis zur ersten Eckfrequenz fu berechnet sich zu
uFB= u ∙ Tp∙f = 5V ∙ 3,04µs ∙ 10kHz = 152mV
Wir werden das Ergebnis gleich mit LT-Spice kontrollieren. Da LT-Spice jedoch in der Berechnung des Spektrums den Effektivwert verwendet, müssen wir das Ergebnis noch mit √2 multiplizieren und in dBV konvertieren.
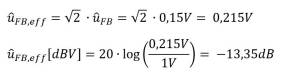
Bevor wir eine Skizze der Einhüllenden Störemissionen im Frequenzbereich erstellen können fehlen uns noch die beiden charakteristischen Frequenzen fu und fo.
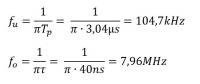
Nachfolgende Abbildung zeigt das mit LT-Spice simulierte Spektrum unseres Impulses im Frequenzbereich zusammen mit der zuvor hergeleiteten Einhüllenden mit den drei charakteristischen Abschnitten.
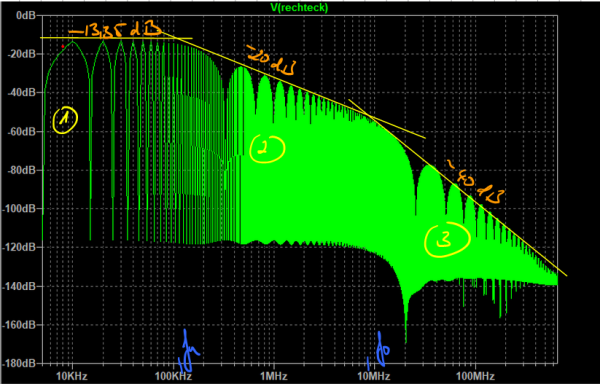
Die Bereiche eins uns zwei stimmen exakt mit dem berechneten Wert überein. Lediglich der dritte Bereich zeigt eine etwas geringere Steigung als die erwarteten -40dB/Dekade, ab einer Frequenz von ca. 100MHz. Dies deutet darauf hin, dass es noch einen vierten Bereich geben muss den wir bisher nicht betrachtet haben. Das ist allerdings auch nicht notwendig, da die Amplituden um mehr als 100dB gedämpft sind und daher im Vergleich zu den zuvor aufgetretenen Frequenzanteile nicht mehr ins Gewicht fallen. Wir werden später sehen, dass in diesem Frequenzbereich dann meist andere Effekte, wie angeregte Serien- oder Parallelschwingkreise, welche über parasitäre Elemente gebildet werden, dominieren.
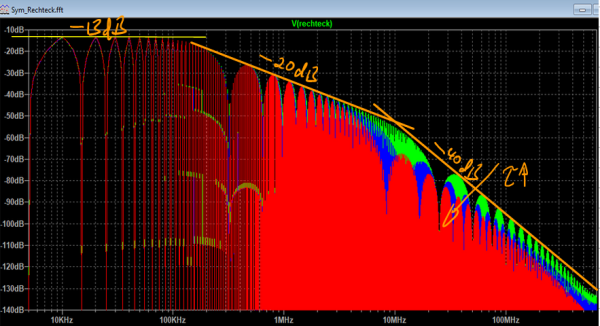
In der Simulation lässt sich der Einfluss der Flankenzeiten auf das Spektrum mit Hilfe einer Parametervariation sehr anschaulich darstellen. Obige Abbildung zeigt die Spektren des Rechteckimpuls für verschiedene Flankenzeiten (40ns, 80ns und 120ns). Wie erwartet können wir durch eine Reduktion der Gradienten du/dt des Impulses die hochfrequenten Anteile im Spektrum stark dämpfen. Der Wunsch nach reduzierten Gradienten aus der EMV steht allerdings im Widerspruch zu den Anforderungen der Hardwareentwicklung. Besonders beim Ein- und Ausschalten von Leistungshalbleitern in der Leistungselektronik ist man bemüht die Schalthandlung so schnell wie möglich abzuschließen um die dabei auftretenden Schaltverluste zu minimieren.
Rechteckimpulse / Messung
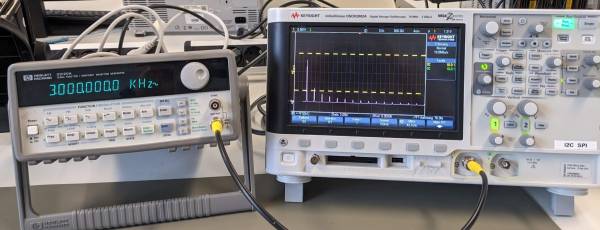
Die bisher theoretisch betrachteten Rechtecksignale werden wir nun messtechnisch charakterisieren. Dazu verbinden Sie den Signalgenerator mit einem Oszilloskop und stellen einen beliebiges Rechtecksignal ein. Machen Sie sich zuerst mit beiden Geräten vertraut und versuchen Sie mehrere Parameter zu variieren.
Aufgabe 4
- Charakterisieren Sie das Rechtecksignal und erstellen Sie eine handschriftliche Skizze mit dem erwarteten Frequenzspektrum.
- Ermitteln Sie mit dem Oszilloskop die Amplituden der ersten fünf Oberschwingungen und vergleichen Sie diese mit Ihre Berechnung.
- Beobachten Sie was passiert sobald das Rechtecksignal unsymmetrisch wird
- Bis zu welcher Frequenz lassen sich die Oberschwingungen mit dem Oszilloskop ermitteln?
Hinweis:
Falls sie Zweifel haben ob Sie mit dem Rechtecksignal korrekte Werte ermitteln im Frequenzbereich verwenden Sie einen noch einfacheren
Impuls zur „Kalibration“ der Messkette.
Spektrumanalyse
Wie Sie sicher festgestellt haben ist es sehr mühsam mit dem Oszilloskop die spektralen Anteile eines Signals zu erfassen. Das ist ja eigentlich auch nicht deren primäre Aufgabe. Oft ist es einfacher die Rohdaten der Messwerte
an Matlab zu übermitteln und die Auswertung der Signale im Frequenzbereich dann dort durchzuführen. Dabei ist allerdings auf allerhand zu achten. Zum Beispiel, dass die richtige Skalierung gewählt wird, Fehler durch Fensterfunktionen und so weiter ….
Je nach Oszilloskop ist vermutlich auch die Eingangsbandbreite der Geräte limitiert.
- Erklären Sie den Begriff Eingangsbandbreite.
- Wann und wozu wird eine Fensterfunktion benötigt?
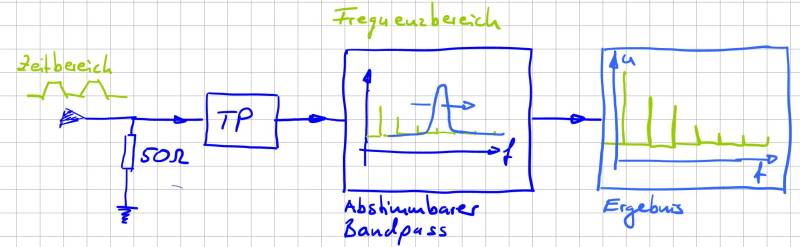
Im Labor haben wir ein Oszilloskop von Rhode&Schwarz welches genau die oben beschriebenen Probleme bei der Messung behebt. Das Gerät besitzt eine sehr große Eingangsbandbreite und bietet zahlreiche Möglichkeiten über eine FFT sich das Spektrum komfortabel anzeigen zu lassen. Eleganter als mit einem Oszilloskop lassen sich die Spektralanteile im Frequenzbereich mit Hilfe eines Spektrumanalysator oder Messempfänger darstellen. Das Spektrum des Eingangssignals wird dabei nicht aus dem Zeitverlauf berechnet, sondern durch Analyse direkt im Frequenzbereich ermittelt. Für eine solche Analyse ist es notwendig,das Eingangsspektrum in seine einzelnen Komponenten zu zerlegen. Am Einfachsten ist die Funktion der Geräte zu erklären wenn man sich einen Bandpass vorstellt, der im Frequenzbereich über unser Spektrum hinwegläuft. Während dessen sammelt der Bandbass die vorhandenen Signalanteile auf, die dann als am Ausgang des Filters abgegriffen werden können. (Siehe nachfolgende Abbildung oder, Video zu Kapitel 3 im EMV-Skript)
Folgende Parameter können bzw. müssen eingestellt werden:
- Frequenzbereich: Der darzustellende Frequenzbereich kann durch Start- und Stopp-Frequenz, also der niedrigsten bzw. höchsten darzustellenden Frequenz, oder durch die Mittenfrequenz (Center Frequency) und den Darstellbereich (Span), zentriert um die Mittenfrequenz, eingestellt werden.
- Frequenzauflösung: Bei Analysatoren die im Frequenzbereich arbeiten kann die Auflösebandbreite (Bandbreite des eingesetzten Bandbass) eingestellt werden. (Resolution Bandwidth, RBW).
- Sweep-Zeit: Die Zeit, die benötigt wird, um das gesamte interessierende Frequenzspektrum aufzunehmen, wird als Sweep-Zeit (Sweep Time) bezeichnet.
- Pegeldarstellbereich: Die Einstellung erfolgt über den maximal darzustellenden Pegel, den sog. Referenzpegel (Reference Level), und den Darstellbereich.
Die Parameter sind nicht unabhängig voneinander. So hat zum Beispiel der betrachtete Frequenzbereich und die Auflösebandbreite natürlich Einfluss darauf wie lange es dauert bis der Bandbass den gesamten Frequenzbereich erfasst hat, also auf die Sweep-Time.
Die Vorstellung, dass ein Bandpass über das
Frequenzspektrum geschoben wird ist eine gute Möglichkeit sich die Funktion der Geräte herzuleiten. Allerdings ist so ein Bandpass über einen großen Frequenzbereich in der Realität nur sehr schwer realisierbar. In Wirklichkeit lässt man den Bandpass einfach bei einer festen Frequenz stehen, der sogenannten
Zwischenfrequenz, und schiebt das betrachtete Signal durch den Bandpass. Mit der konstanten Bandbreite und Mittenfrequenz des Bandpass lässt sich dieser sehr exakt und stabil aufbauen. Variable Oszillatoren bzw. Sinusförmige Quellen lassen sich hingegen einfacher aufbauen. Über einen Mischer wird das Eingangssignal mit dem
Signal es variablen Oszillators multipliziert und damit in das Fenster unseres Bandbpass geschoben.
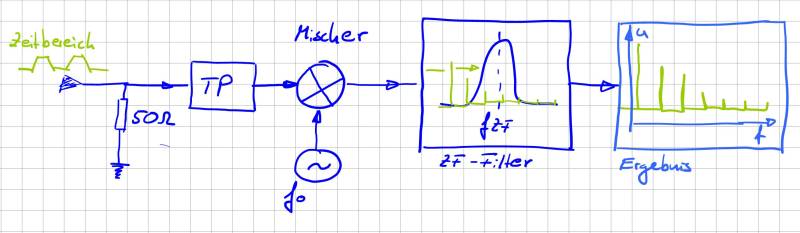
Dieses Verfahren wird auch Überlagerungsprinzip oder Heterodyn-Prinzip bezeichnet. Weitere Informationen findet man zum Beispiel als Application Note von Rohde&Schwarz „Messen mit modernen Spektrumanalysatoren“ oder wenn man nach „Grundlagen der Spektrumanalyse“ googelt findet man das Buch von Christoph Rauscher als pdf welches einen guten Überblick zu den Messverfahren gibt.
Achtung, 50Ω
 Bevor wir uns den Spektrumanalysatoren nähern, müssen wir uns die Eingangsbeschaltung anschauen. Um Reflexionen und Fehlanpassungen am Leitungsende zu vermeiden (siehe, letzte Aufgabe) sind die Eingänge
der Messgeräte typischerweise mit 50Ω terminiert. Das kommt daher, dass Koaxialleiter in der Messtechnik einen Wellenwiderstand von 50Ω aufweisen. In der Rundfunk und Fernsehtechnik sind 75Ω Systeme im Einsatz.
Für einen Wechsel der Impedanzen sind von den Herstellern Anpassnetzwerke verfügbar. Wichtiger als die Eingangsimpedanz sind allerdings die weiteren Angaben auf der Warntafel. 0V DC bedeutet, dass keine Gleichspannung
an das Messgerät angelegt werden darf. Wozu auch, der Gleichspannungsanteil bzw. die Amplitude für f = 0Hz interessiert uns in der EMV nie. Eine Gleichspannung würde die Eingangsbeschaltung vermutlich sehr schnell zerstören.
Daher keinesfalls den Funktionsgenerator direkt mit dem Analysator verbinden. Die Warntafel deutet mit DC Coupled weiter darauf hin, dass keine Schutz gegenüber Gleichströmen bzw. ein Hochpassfilter implementiert ist.
Das ist unsere Aufgabe. Generell gilt, falls Sie sich nicht sicher sind lieber einen sogenannten DC-Block verwenden. Das ist einfach ein Kondensator in Serienschaltung als Hochpassfilter. Er verhindert, dass ein Gleichstrom
fließen kann.
Bevor wir uns den Spektrumanalysatoren nähern, müssen wir uns die Eingangsbeschaltung anschauen. Um Reflexionen und Fehlanpassungen am Leitungsende zu vermeiden (siehe, letzte Aufgabe) sind die Eingänge
der Messgeräte typischerweise mit 50Ω terminiert. Das kommt daher, dass Koaxialleiter in der Messtechnik einen Wellenwiderstand von 50Ω aufweisen. In der Rundfunk und Fernsehtechnik sind 75Ω Systeme im Einsatz.
Für einen Wechsel der Impedanzen sind von den Herstellern Anpassnetzwerke verfügbar. Wichtiger als die Eingangsimpedanz sind allerdings die weiteren Angaben auf der Warntafel. 0V DC bedeutet, dass keine Gleichspannung
an das Messgerät angelegt werden darf. Wozu auch, der Gleichspannungsanteil bzw. die Amplitude für f = 0Hz interessiert uns in der EMV nie. Eine Gleichspannung würde die Eingangsbeschaltung vermutlich sehr schnell zerstören.
Daher keinesfalls den Funktionsgenerator direkt mit dem Analysator verbinden. Die Warntafel deutet mit DC Coupled weiter darauf hin, dass keine Schutz gegenüber Gleichströmen bzw. ein Hochpassfilter implementiert ist.
Das ist unsere Aufgabe. Generell gilt, falls Sie sich nicht sicher sind lieber einen sogenannten DC-Block verwenden. Das ist einfach ein Kondensator in Serienschaltung als Hochpassfilter. Er verhindert, dass ein Gleichstrom
fließen kann.
Die letzte Angabe auf dem Warnschild zeigt uns an wie viel Leistung der 50Ω Abschlusswiderstand aufnehmen kann. Ganz EMV-Typisch natürlich in dBm angegeben. Aus der maximalen Leistungsangabe von +30dBm können wir berechnen, welchen maximalen
Spannungspegel wir an die Eingangsbeschaltung anlegen dürfen ohne diese zu schädigen. Nachfolgende Herleitung hilft uns diesen Wert in Abhängigkeit der Spannungsamplitude zu berechnen.
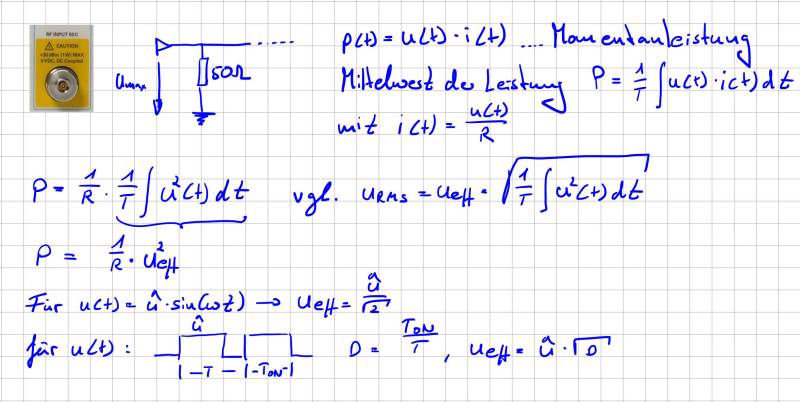
Wie gezeigt und vermutet ist dieser Wert abhängig von der Kurvenform. Da die Messgeräte sehr teuer sind sollte es allerdings niemals unser Ziel sein den Eingangsspannungsbereich voll auszureizen. Meist haben die Geräte eine derart hohe Dynamik (Pegelauflösung) damit wir ohne Sorge ein sogenanntes Dämpfungsglied z.B. 10dB oder 20dB einsetzen können.
Aufgabe 5
- Berechnen Sie für eine rein sinusförmige Anregung den maximalen Spannungspegel den Sie an das Gerät anlegen dürfen
- Berechnen Sie den maximalen Spitzenwert eines mittelwertfreien, symmetrischen Rechtecksignal das Sie an das Gerät anlegen dürfen
Messen gestrahlter Emissionen
Einleitung
Die Messung der gestrahlten Emission einer Komponente ist das Bild das viele von uns vor Augen haben wenn wir an die elektromagnetische Verträglichkeit denken.
Sicher liegen darin auch die Ursprünge EMV. Das klassische Problem: Durch eine elektromagnetische Kopplung werden Geräte gestört. Oder anders ausgedrückt, ein von einem Gerät A ausgehende
elektromagnetische Welle koppelt in ein Gerät B ein und macht dort Unfug. Das kann soweit führen, dass Gerät B ausfällt oder nicht mehr ordnungsgemäß funktioniert.
Der Gesetzgeber hat reagiert und für diese Emissionen Grenzwerte festgelegt welche nicht überschritten werden dürfen.
ACHTUNG: Falls Sie nicht sicher sind ob die maximal zulässige Spannung am Eingang des Messgeräts überschritten wird oder ob ein Gleichspannungsanteil im Signal vorhanden ist, fragen Sie nach oder benutzen Sie vorsichtshalber einen DC-Block!
Was liegt wohl alles in der Luft?
Um die Messgeräte besser kennenzulernen ermitteln wir mit Hilfe einer Antenne und dem Spektrumanalysator die empfangbaren Rundfunk oder Mobilfunkfrequenzen. Verbinden Sie dazu im ersten Schritt die Antenne mit dem Messgerät. Überlegen Sie sich welchen Frequenzbereich Sie analysieren möchten.
Klickanleitung
Diese Anleitung soll eine kurze Einführung in Einstellung und Messung mit dem Spektrumanalysator / Messempfänger geben. Ziel ist es mit einer Antenne Radiofrequenzen zu erfassen. Zuerst wird überprüft ob der Spektralanalysator im richtigen Modus arbeitet.
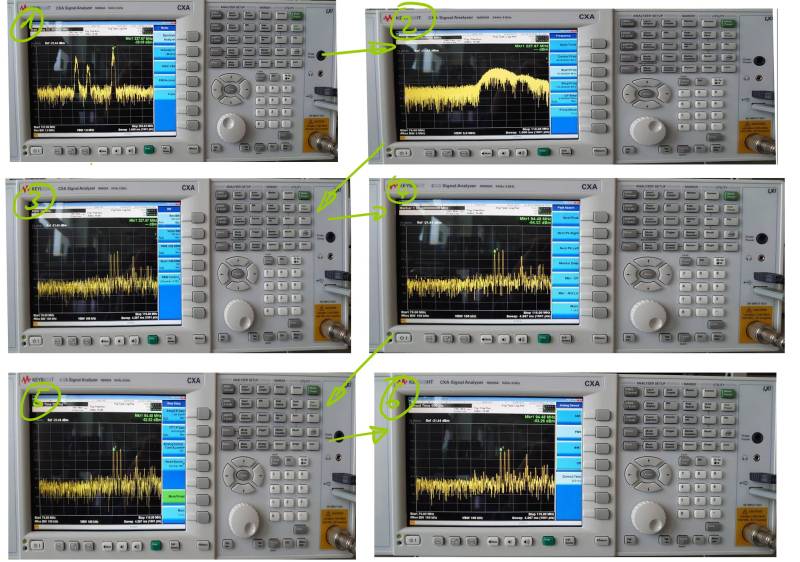
- Dazu wird der Button „Mode“ gedrückt und die Option „Spectrum Analyzer“ eingestellt.
- Daraufhin sollte mit dem Button „FREQ Channel“ das Frequenz Menü geöffnet werden. Dort sind die Optionen für das Einstellen der Start- und Stop-Frequenzen zu finden. Damit wird das Frequenzband eingestellt welches überwacht werden soll. Die Einstellung erfolgt mithilfe der Nummern Tasten.
- Im nächsten Schritt muss die Brandbreite eingestellt werden mit welcher der Frequenzbereich durchgegangen wird. Dazu muss das Menü „BW“ mit der Taste „BW“ aufgerufen werden. Um die Radiofrequenzen zu erfassen, wurde die „Res. BW“ auf 100kHz eingestellt.
- Nun kann im Marker Bereich der Button „Peak Search“ angewählt werden. Damit platziert das Messgerät einen Marker an einem der Peaks im Frequenzbereich. Dieser Marker kann entweder mit dem Stellrad oder mit der Option „Next Pk Right/Left“ an einen weiteren Peak rechts bzw. links von dem bisherigen verschoben werden. Da es in dem Beispiel ein Radiosignal zu erfassen gilt, wird der Marker auf eine bekannte Radiofrequenz eingestellt.
- Als Nächstes muss das gewählte Radiosignal demoduliert werden. Dazu wird in des Messungsmenü mit dem Button „Meas Setup“ gewechselt. Um die Option der Demodulierung zu finden, muss mit der „More“ Option die zweite Seite des Menüs geöffnet werden. Nun wird „AnalogDemod Tune&Listen“ ausgewählt.
- Daraufhin muss noch die Art der Demodulation gewählt werden. Um Radio zu hören wird die Demodulation „FM“ gewählt.
- Nun sollte das Messgerät einen Ton ausgeben. Mit den Lautsprechertasten unterhalb der Anzeige kann die Lautstärke eingestellt werden. Damit ist nun das Beispiel abgeschlossen.
In vielen Fällen will man mit dem Messgerät jedoch etwas auf Störeinkopplungen bzw. Aussendungen überprüfen. Besonders auf das Einhalten der EMV-Normen wird Wert gelegt. Dankenswerter Weise sind bestimme EMV-Normen bereits im Messgerät eingespeichert. Damit muss man sich keine Gedanken machen um die korrekte Einstellung des Frequenzbereichs oder der Bandweite.
- Um eine Voreinstellung auszuwählen muss wieder mir der Taste „Mode“ das „Mode Setup“ geöffnet werden. Unter „EMC Standard“ wird nun die Art der EMV-Norm ausgewählt. Für den Laboraufbau wird sich auf die CISPR Normen bezogen.
- Nun kann mit der Option „CISPR Presets“ die gewollte Voreinstellung ausgewählt werden.
Aufgabe 6
- Finden Sie im ersten Schritt heraus ob der Analysator Spitzen- oder Effektivwerte anzeigt.
- Lassen Sie sich die mit der Antenne messbaren Rundfunkfrequenzen anzeigen und demodulieren Sie einen Radiosender
- Ermitteln Sie den Spitzenwert der an der Antenne (Antennfenfußpunkt) anliegenden Spannung
Teil 2 Tiefsetzsteller
Funktionsbeschreibung
Ich möchte Ihnen eine Schaltung vorstellen welche als Grundschaltung jeder Leistungselektronik angesehen werden kann und welche den zuvor eingeführten Rechteckimpuls zur Funktion benötigt. Die Rede ist vom sogenannten Tiefsetzsteller (engl. Buck-Converter). Tiefsetzsteller sind heutzutage in nahezu allen elektronischen Geräten verbaut. Sie passen die DC-Versorgungsspannung auf die jeweilige Anwendung an, zum Beispiel für Mikrocontroller, als LED-Treiber, für Displays und viele mehr. Die Ausgangsspannung ist dabei stets kleiner oder maximal gleich groß wie die Eingangsspannung.
\\:
Dabei gilt
Ausgangsspannung UAus = D∙UEin, D x Eingangsspannung
D bezeichnet den sogenannten Tastgrad oder auch Duty-Cycle. Er definiert das Verhältnis zwischen Einschaltzeit (Ton) und Periodendauer (T) eines Rechtecksignals. Ein Tastgrad von 50% entspricht dem uns bereits bekannten symmetrischen Rechtecksignal. Nachfolgende Abbildung zeigt die Rechteckimpulse bei verschiedenem Duty-Cycle oder auf deutsch für verschiedene Puls-Pausenverhaltnisse (oder auch als Tastgrad bezeichnet).
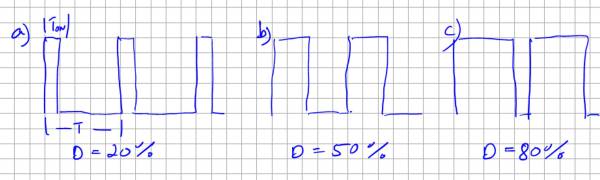
Die Gleichung zeigt, dass sich über den Tastgrad komfortabel die Ausgangsspannung UAus einstellen lässt. Die Hardware des Tiefsetzstellers besteht dabei aus nur wenigen Elementen, einem Schaltelement S zum Ein- und Ausschalten des Stromflusses, einer Induktivität L als Zwischenspeicher und einer Freilaufdiode D welche einen kontinuierlichen Stromfluss gewährleistet. Zur Glättung der Ausgangsspannung wird typischerweise ein Glättungskondensator am Ausgang hinzugefügt. Das Schaltelement wird mit Hilfe der Pulsweitenmodulation angesteuert und entscheidet somit über die aus der Quelle entnommene Leistung.
Nachfolgende Abbildung zeigt den Stromfluss innerhalb der Schaltung je nach Zustand des Schaltelements. Wird der Schalter S geschlossen fließt der Strom in der großen Schleife durch die Last RL zurück in die Quelle. Da der Stromfluss durch eine Induktivität kontinuierlich sein muss fließt der Strom bei geöffnetem Schalter S durch die Freilaufdiode, die kleine Schleife im Bild in Grün dargestellt. Wir sprechen dabei davon, dass der Strom auf die Freilaufdiode kommutiert.
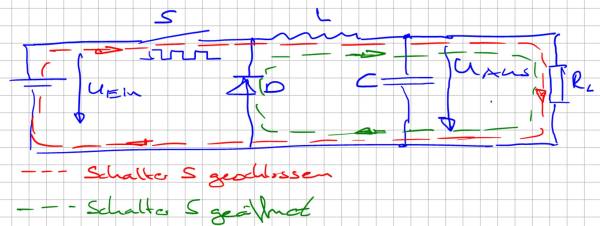
Jetzt aber zum eigentlichen Problem. Dazu schauen wir uns den Strom durch das Schaltelement S bzw. die Batterie am Eingang genauer an. Der Eingangsstrom in den Tiefsetzsteller ist gezwungen direkt dem Schalterzustand zu folgen, also entsprechend dem Ansteuersignal. Damit übergeben wird die Rechtecksignale und deren Oberschwingungen direkt auf die Zuleitungen. Nachfolgende Abbildung zeigt ein Simulationsbeispiel aus LT-Spice mit dem dazugehörigen Eingangsstrom im Zeit- und Frequenzbereich. Die Schaltung könnte so in einer Anwendung eingesetzt werden welche in einem Fahrzeug aus einer Batterie die Versorgungsspannung für einen Mikrocontroller bereitstellt.
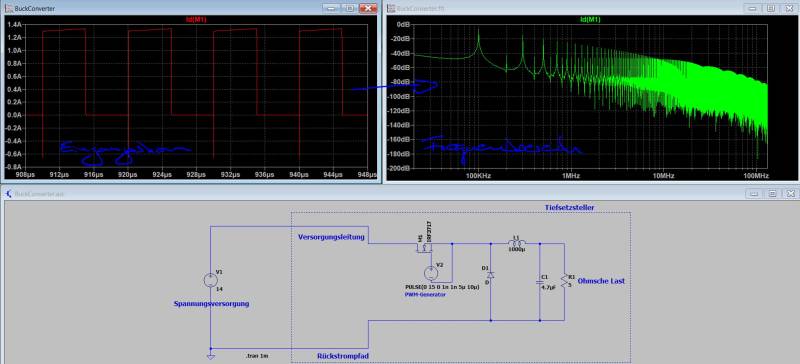
Wie wir später sehen werden, in einer Simulation zu den leitungsgebundenen Störungen, müssen wir das Ergebnis noch als Störspannung interpretieren. Mir ist an dieser Stelle nicht wichtig einen direkten Vergleich mit dem Grenzwert herzuleiten, sondern vielmehr zu zeigen, dass jegliche Art von Elektronik welche Ströme schaltet ohne eine Filterschaltung nicht betrieben werden kann. Die in obiger Abbildung berechneten Oberschwingungen werden ansonsten auf den Versorgungsleitungen sichtbar und sich zu allen am Netz angeschlossenen Verbraucher aus. Aufgrund der hohen Elektronikdichte in modernen Kraftfahrzeugen muss hier besonders genau auf die von den einzelnen Steuergeräten generierten Emissionen geachtet werden. Die im Strom sichtbaren Oberschwingungen folgen den Oberschwingungen unseres Rechtecksignals. Eine symmetrische Anregung des Schalters (50% Duty) ohne die geradzahligen Oberschwingungen in dessen Spektrum wird auch ein Stromsignal ohne geradzahlige Oberschwingungen generieren. Da die Simulation den Schalter mit 100kHz anregt ist dies in Bild 2.15 schön zu sehen durch die hohe Dämpfung der Oberschwingungen bei 200kHz, 400kHz usw.. Zusammenfassend lässt sich feststellen, dass sämtliche getakteten Systeme eine unendliche Anzahl an hochfrequenten Signalen generieren. Unsere Aufgabe als EMV-Ingenieur ist es diese hochfrequenten Anteile soweit zu dämpfen, dass Sie abgesehen von deren funktionalen Eigenschaften keinen Schaden anrichten können.
Es schwingt
Mit dem Rechteckimpuls kennen wir die wichtigste Quelle hochfrequenter Signale. Reale Schaltungen verwenden natürlich eine Reihe weitere Signale mit dreieck- oder trapezförmigem Verlauf bzw. einer beliebigen Kombination daraus. Alle diese Signale lassen sich mit Hilfe der EMV-Tafel auf unser einhüllendes Spektrum zurückführen. Es bleibt daher die Frage: Warum folgen Emissionsmessungen nicht prinzipiell dem Verlauf der Einhüllenden aus der EMV-Tafel? Wir haben bereits in einführenden Beispielen gesehen, die Emissionen in höheren Frequenzbereichen stark ansteigen können. Eine häufige Ursache dieser Anstiege sind Schwingkreise welche durch unsere periodischen Signale angeregt werden.
Schwingkreise entstehen immer dann, wenn Kapazitäten auf Induktivitäten treffen. Beide Bauteile können elektrische Energie speichern. Kapazitäten nutzen hierzu elektrische Felder, Induktivitäten das magnetische Feld. Wenn wir ausdrücken welcher elektrische Widerstand die Bauelemente dem hochfrequenten Strom entgegensetzen sprechen wir von Impedanzen. Wir sagen dann zum Beispiel, ein Kondensator besitzt an der Frequenz 10MHz eine Impedanz von 5Ω. In Schwingkreisen pendelt die elektrische Energie zwischen diesen beiden Energiespeichern hin und her. Das Maximum dieser Pendelbewegung wird erreicht an der Resonanzfrequenz fR, hier ist die Impedanz der Kapazität gleich groß wie die der Induktivität.
An der Resonanzfrequenz ist die Impedanz von Induktivität und Kapazität gleich groß, sie heben sich auf!
Die Resonanzfrequenz ist für uns kritisch, da es hier zu einer Spannungs- oder Stromüberhöhung kommen kann. Dieser bei uns auf der Leiterkarte oder im Aufbau ungewollte Effekt wird in anderen Bereichen der Elektrotechnik, zum Beispiel in der Hochspannungsprüftechnik zur Erzeugung hoher Prüfspannungen, sehr häufig eingesetzt. Die für einen Schwingkreis notwendige Kapazität und Induktivität besteht überwiegend nicht aus diskreten (auf der Platine oder im Aufbau geplanten) Bauelementen, sondern vielmehr aus den sogenannten parasitären Eigenschaften des Aufbaus bzw. der verwendeten Komponenten. Ganz allgemein lässt sich sagen, zwischen allen Knotenpunkten einer elektrischen Schaltung bilden sich Kapazitäten aus, jeder Strompfad bildet eine Induktivität. Oder etwas spezifischer:
- An jeder Stelle mit einer Potenzialdifferenz kann man sich gedanklich eine Kapazität denken
- Jeder stromdurchflossene Leiter bildet ein Magnetfeld und damit eine Induktivität
Wenn wir an die Vielzahl an unterschiedlichen Potenzialen in unserer Schaltung denken und die Menge an Leitungsverbindungen, stellen wir schnell fest, dass es eine hohe Anzahl an schwingfähigen Gebilden geben muss in unseren Systemen. Viele davon sind allerdings so gering, dass sie sich kaum bemerkbar machen. Andere hingegen dominieren den Emissionsverlauf in weiten Bereichen des Frequenzbereichs.
In der Literatur findet man parasitäre Kapazitäten und Induktivitäten auch unter dem Begriff Streukapazität bzw. Streuinduktivität.
Die Impedanz einer beliebigen Kapazität berechnet sich zu ZC= 1/ωC , die Impedanz einer Induktivität zu ZL= ωL. An diesen Gleichungen lässt sich bereits jetzt erkennen, dass beide Bauteile unsere wichtigsten Verbündeten zur Reduktion hochfrequenter Signale sind. Aufgrund der wachsenden Impedanz bei steigender Frequenz, können mit Induktivitäten hochfrequente Störströme reduziert werden. In einer Serienschaltung verhindern wird damit deren Ausbreitung. Kapazitäten hingegen können verwendet werden die hochfrequenten Anteile kurzzuschließen bzw. gegen die Masse abzuleiten, da deren Impedanz mit steigender Frequenz mit 1/f abnimmt. Nachfolgende Abbildung zeigt den Verlauf der Impedanz über der Frequenz idealer Kapazitäten und Induktivitäten.
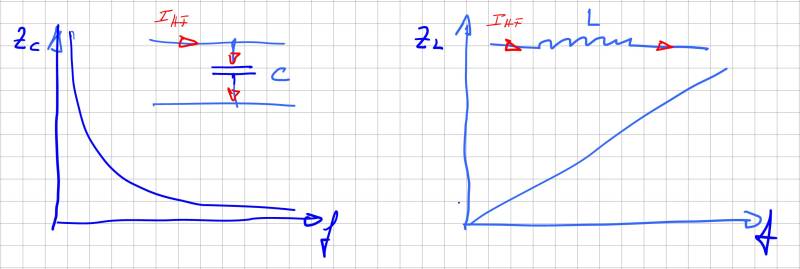
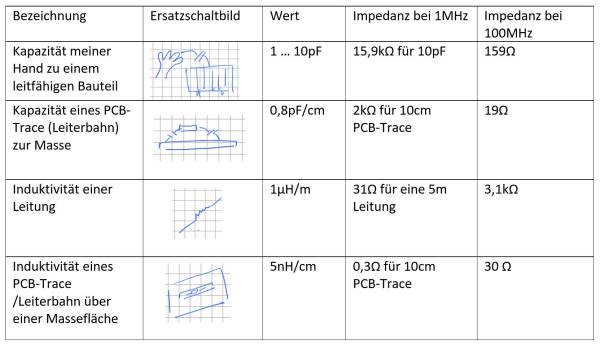
Um ein Gefühl dafür zu bekommen in welcher Größenordnung wir uns bewegen, einige Beispiele ausgewählter Kapazitäten und Induktivitäten.
An der Resonanzfrequenz fR sind beide Impedanzen (der Kapazität und der Induktivität) gleich groß und es gilt:
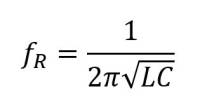
Wir sehen, je kleiner die Kapazitäts- und Induktivitätswerte, desto höherfrequent ist die auftretende Resonanzfrequenz. Die Gleichung gilt übrigens sowohl für den Serien- als auch den Parallelschwingkreis.
Schauen wir uns jetzt ein Beispiel für die Auswirkungen von Schwingkreisen an. Den einfachen Tiefsetzsteller mit seiner periodischen Anregung haben wir ja bereits kennengelernt. Ihn erweitern wir jetzt um eine Induktivität Ls, welche ein kurzes Stück einer Leiterbahn darstellen soll. Die gewählten 10nH entsprechen einer Verbindungslänge zum Knotenpunkt A von ca. 2cm Länge. Nachfolgende Abbildung zeigt den erweiterten Schaltplan. Darin sind die Bauelemente markiert, welche den Schwingkreis bilden.
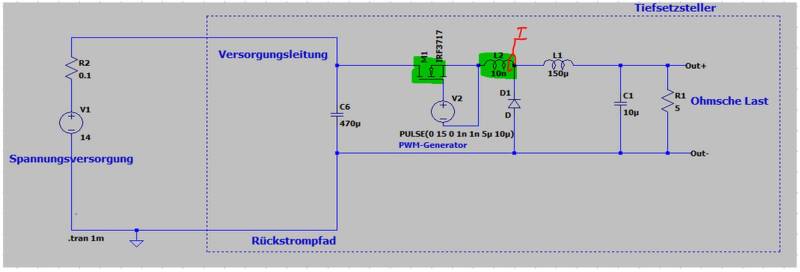
Um die Schwingung zu bewerten messen wir den Strom Is durch die parasitäre Induktivität, welcher gleichzeitig auch dem Strom durch unseren Leistungsschalter (Drain-Strom des Mosfets) entspricht. In nachfolgender Abbildung ist die sich ausbildende Schwingung beim Abschalten des Mosfets deutlich zu erkennen.
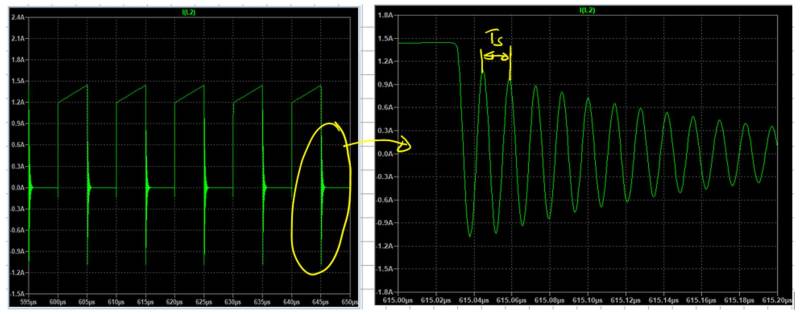
Mit Hilfe der Cursor-Funktion in LT-Spice ermitteln wir die Schwingungsdauer Ts zu 14ns woraus sich eine Frequenz fR von 72MHz ergibt. Die Resonanzfrequenz tritt natürlich im Frequenzspektrum deutlich hervor, welches sich durch die Berechnung der FFT-Funktion anzeigen lässt,
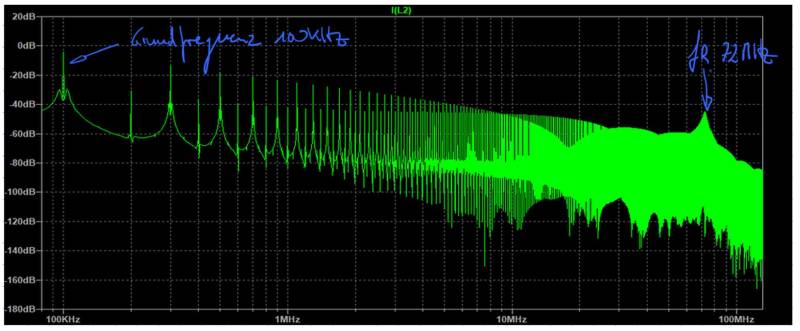
Aus der Resonanzfrequenz und der in unserem Beispiel bekannten Induktivität des Schwingkreises lässt sich der Kapazitätswert berechnen aus:

Dieser Wert deckt sich in seiner Größenordnung mit den Angaben zu den parasitären Kapazitäten des Mofets IRF3717 aus dessen Datenblatt. Zu beachten ist, dass die Angaben im Datenblatt nur zu einem speziellen Betriebspunkt und der dazugehörigen Testschaltung gehören. Ein Vergleich zu anderen Betriebspunkten ist nur bedingt möglich, da die Streukapazitäten von der Höhe der angelegten Spannung abhängig sind.

Um einen Kapazitätswert im pF- Bereich (1×10-12) von seiner Größe her einzuordnen erinnern wir uns zurück in den Physikunterricht unserer Schulzeit. Dort gab es meist große Plattenkondensatoren für einfache Versuche mit einer Kapazität. Um eine Kapazität von 10pF mit Hilfe eines Plattenkondensators herzustellen benötigen wir lediglich Platten mit einer Seitenlänge von 3,4cm, bei einem Plattenabstand von 1cm, umringt von Luft. Sie erinnern sich vielleicht, dass sich die Kapazität massiv steigern lässt durch das Einbringen eines Dielektrikums. Das bedeutet, Kapazitäten im Bereich von wenigen pF entstehen nahezu überall zwischen geometrischen Strukturen. Insbesondere innerhalb dielektrischer Materialien steigt deren Kapazität massiv an. Dieser Effekt ist bei Halbleitern und meist isolierenden Medien (Klebstoffen, Vergussmassen) zu beobachten.
Unser einfaches Beispiel mit nur einer dominanten Resonanzfrequenz kann natürlich nicht den komplexen Aufbau einer realen Schaltung abbilden. Hier gibt es eine Vielzahl unterschiedlicher Schwingkreise, die angeregt werden können. Bei Messungen zur Störemissionsmessung dominieren meist zwei bis drei Schwingkreise den Emissionspegel. Die Resonanzfrequenzen der weitern Schwingkreise werden dabei durch die Pegel der dominanten Schwingkreise überdeckt und tauchen erst dann auf, falls es uns gelingt diese mit geeigneten EMV-Maßnahmen zu reduzieren.
Aufgabe 7
- Erstellen Sie eine einfache funktionale Simulation des Tiefsetzstellers wie im gezeigten Beispiel und betrachten Sie das Spektrum des Stromes
- Fügen Sie an verschiedenen Stellen parasitäre Leitungsinduktivitäten ein und überprüfen Sie ob sich Schwingkreise ausbilden. Unterscheiden Sie zwischen „guten“ und „schlechten“ parasitären Induktivitäten.
- Stellen Sie eine parasitäre Induktivität so ein, dass sich eine Resonanz bei ca. 50MHz ergibt.
Messung leitungsgebundener Emissionen
Unser Simulationsbeispiel des Tiefsetzstellers haben wir im Frequenzbereich bewertet über den Strom der durch den Mosfet fließt. Dem Gesetzgeber ist es allerdings ziemlich egal, welche internen Ströme intern fließen und ob sich innerhalb der Geräte hochfrequente Resonanzkreise ausbilden. Wichtig ist, dass davon nichts nach außen dringen kann. Weder über gestrahlte Emissionen, in Form elektromagnetischer Wellen, noch über die Versorgungsleitungen. Bei Störungen auf den Versorgungsleitungen sprechen wir von „leitungsgebundenen Emissionen“. Besonders in hochintegrierten Systemen, wie modernen Kraftfahrzeugen mit sehr vielen Steuergeräten, muss dieser Art der Störung besondere Aufmerksamkeit geschenkt werden. Gelangen die Störungen auf diesem Pfad in das System erreichen sie alle weiteren angeschlossenen Steuergeräte und können so massiven Schaden anrichten.
Zur Auskopplung der Störströme werden sogenannte Netznachbildungen verwendet. Ihre Aufgabe ist es die auf den Versorgungsleitungen fließenden Störströme auszukoppeln und einem Messgerät (Oszilloskop oder Netznachbildung) zuzuführen. Bitte schauen Sie sich dazu im Skript zur Vorlesung EMV das Kapitel 2.3 an.
Für unsere Laborarbeit verwenden wir folgende Netznachbildung:
 (Bild: Elektor Magazin) Diese Art der Netznachbildung kann für Messungen nach der CISPR25 bzw. DIN EN55025 verwendet werden. Sie besitzt bereits ein integriertes 10dB Dämpfungsgrlied welches bei der Messung entsprechend addiert werden muss. Im Labor haben wir noch eine zweite Variante (Entstanden in einer Abschlussarbeit) ohne integriertes Dämpfungsglied.
(Bild: Elektor Magazin) Diese Art der Netznachbildung kann für Messungen nach der CISPR25 bzw. DIN EN55025 verwendet werden. Sie besitzt bereits ein integriertes 10dB Dämpfungsgrlied welches bei der Messung entsprechend addiert werden muss. Im Labor haben wir noch eine zweite Variante (Entstanden in einer Abschlussarbeit) ohne integriertes Dämpfungsglied.
Innerhalb des Hochschulnetz (alternativ mit VPN-Verbindung) haben wir Zugang zu allen DIN EN Normen über den Link: Datenbank-Infosystem (DBIS)
Aufgabe 8
Wir haben die Chance unseren Tiefsetzsteller als Sitzheizung einem Fahrzeughersteller zu verkaufen. Unser Kunde verlangt allerdings bereits in der Entwicklungsphase Nachweise welche Maßnahmen wir zur Einhaltung der EMV treffen.
- Recherchieren Sie den normgerechten Aufbau zur Messung der leitungsgebundenen Emissionen und erstellen Sie eine Skizze.
- Welche Grenzwerte gelten für unsren Tiefsetzsteller?
- Erweitern Sie Ihre Simulation des Tiefsetzstellers um die Netznachbildungen.
Um Vertrauen in das neue Messmittel zu bekommen sollten wir ein bekanntes Signal messen:
- Schließen Sie einen Signalgenerator an die Netznachbildung an und messen Sie die Emissionen mit Hilfe eines Oszilloskiops oder Spektrumanalysator.
- Entspricht das Ergebnis Ihren Erwartungen? Falls nicht, versuchen Sie das Problem mit Hilfe einer einfachen Simulation zu lösen.
Teil3: Tiefsetzsteller / Hardwareaufbau
Im nächsten Schritt schauen wir die Hardware zum Versuch an. Die Schaltung enthält einen einfachen Tiefsetzsteller an dessen Ausgang ein Leistungswiderstand (PTC-Heizelement) angeschlossen ist (Nachbildung der Sitzheizung).
Das Pulsweitenverhältnis kann entweder über den bekannten Timerbaustein NE555 eingestellt werden oder über einen kleinen Mikrocontroller. Die Auswahl wird über Jumper eingestellt.
Dadurch haben wir die Möglichkeit unsere Sitzheizungssteuerung in verschiedenen Versionen unseren Kunden anzubieten:
Die Basisversion stellt die Wärmeleistung im Heizelement stufenlos ein und kann als günstige analoge Einstiegsversion angesehen werden. In der Premiumvariante kann sowohl die PWM-Frequenz als auch die Wärmemenge digital eingestellt werden. Zusätzlich werden wichtige Parameter
auf einem Display ausgegeben welches für die spätere Anwendung appliziert werden kann.
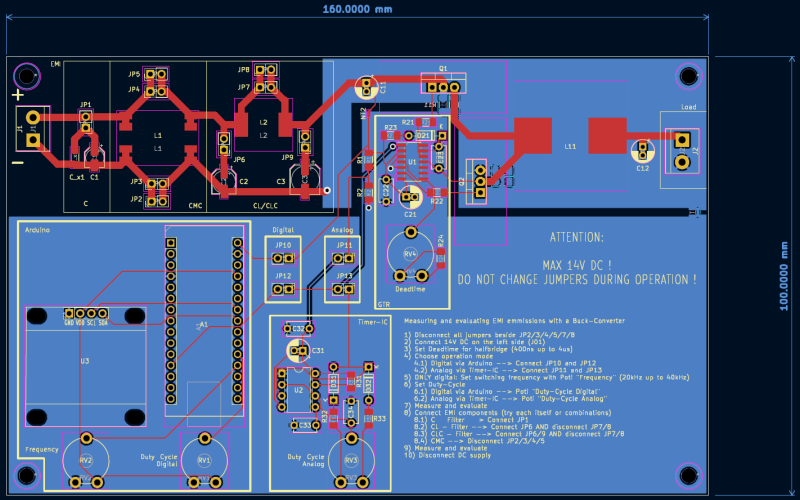
Nachfolgende Abbildung zeigt den fertigen Aufbau der Platine.

ACHTUNG: Auf dem Bild ist der Arduino falsch herum aufgesteckt!!! Dummybild …
Die Platine enthält einige Jumper zur Aktivierung/Deaktivierung einzelner Filterelemente, sowie der Auswahl der Steuerung über den Timer-IC oder über den Arduino. Da ein Jumper entsprechend dem Datenblatt nur etwa drei Ampere tragen kann, werden zur Überbrückung der Gleichtaktspule (CMC) bzw der Spule jeweils zwei Jumper parallell geschlatet. Über einen Net-Tie wird die Trennung des Leistungs- und Logikpfad umgesetzt.
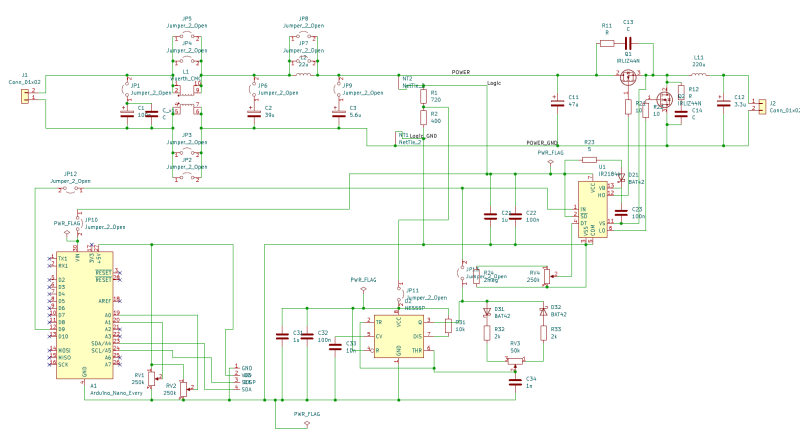
Infos zu den einzelnen Bauelemente können über den Distributor abgerufen werden: bestellung_mouser.xls; bestellung_reichelt.xls
Das Platinen-Layout bietet in der EMV immer Ausbreitungs- und Einkoppelpfade an. Deshalb gibt es hier bereits Maßnahmen um negative Auswirkungen zu minimieren. Prinzipiell gilt es, kritische Pfade (Hochstrom, Hochfrequenz, …) möglichst kurz zu halten. Große Schleifen sollten vermieden werden um vor allem induktive Einkopplungen zu vermeiden. Dies wurde für die Ansteuerung über den Arudino und den Timer-IC nur bedingt eingehalten, da die Platine auch übersichtlich und zugänglich für Änderungen über die Potentiometer sein soll. Ebenfalls sollte der EMV-Filter mit seinen einzelnen Bestandteilen per Hand über die Jumper zuschaltbar sein. Für die Platine wurden trotzdem bereits mehrere gängige Maßnahmen im Layout berücksichtigt, um die Emmissionen der Schaltung zu reduzieren. Diese werden im folgenden kurz aufgelistet:
- Trennung des Leistungpfad und des Logikpfad: Teilung der Masseflächen in Power-Ground und Logic-Ground
- Vorhalt eines RC-Snubbers zur Bedämpfung der Überschwingungen am MOSFET
- Stützkondensatoren/Bypasskondensatoren möglichst nahe am betroffenen Baustein
- Verbindung der Masseflächen an einer ruhigen Stelle
- EMV-Filter ohne Massefläche um galvanisch Weg durch den Filter zu erzwingen
Falls Sie das Layout im CAD anschauen möchten und KiCAD installiert haben: emv_projekt.zip
(Alte Version: kicad_emv_projekt.zip)
Sicherlich wurde der Platz nicht optimal ausgenutzt, dies ist aber auch der komfortablen Nutzung der Platine geschuldet. Sehr gut zu erkennen ist der Platzbedarf des EMV-Eingangsfilters. Es ist üblich bereits zu Entwicklungsbeginn etwa ein Drittel des verfügbaren Bauraum bzw. der Platine als Vorhalt für EMV-Maßnahmen zu berücksichtigen.
Gate- Treiber
Unseren einfachen Tiefsetzsteller haben wir in der Simulation und im Erklärmodell mit einer Freilaufdiode ausgestattet. Das ist prinzipiell richtig, allerdings wird zur Reduktion der Durchlassverluste (an einer Diode fällt ja stets die Vorwärtsspannung ab) die Diode durch einen zweiten Mosfet ersetzt. Dadurch ergibt sich die typische und oft eingesetzte Halbbrücken-Konfiguration. Mosfets kann man sich als spannungsgesteuerte Schalter vorstellen. Wird eine positive Spannung zwischen den Anschlüssen Gate und Source angelegt, kann ein Strom (positiv wie negativ) durch den Mosfet fließen (Drainstrom, zwischen Drain und Source). Nachteilig in dieser Konfiguration ist, dass das Source-Potential des oberen Mosfet (High-Side Mosfet) nicht auf Masse liegt. Um diesen Mosfet zu aktivieren müssen wir uns eine Trick einfallen lassen:
Sehr häufig werden dazu sogenannte Boot-Strap Treiber eingesetzt. Das sind fertige IC-Lösungen welche zum aktivieren des High-Side Mosfet einen geladenen Kondensator (Boot-Strap Kondensator) mit Gate und Source verbindet. Dadurch wird der Mosfet aktiviert. Während der „Aus-Phasen“ des High-Side Mosfet wird dieser Kondensator wieder nachgeladen und ist dann für den nächsten Einschaltvorgang bereit.
Nachfolgende Abbildung zeigt die Grundschaltung der Bootstrap-Schaltung aus dem Datenblatt. Das zentrale Element ist der Bootstrap-Kondensator (Grün markiert) mit dessen Ladepfad (Orange).
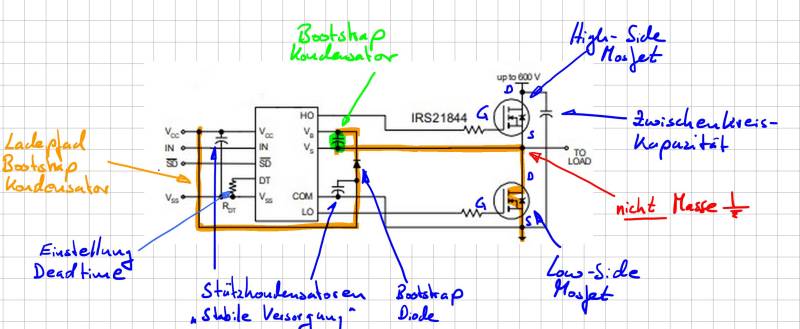
In unserem Beispiel wird durch den Steuereingang „IN“ ein Logikpegel angelegt welcher direkt den High-Side Mosfet aktiviert. Gleichzeitig zu einer Aktivierung des High-Side Mosfet muss der Low-Side Mosfet deaktiviert werden da sich ansonsten eine direkter Kurzschluss der Spannungsversorgung ergeben würde. Ein sogenannter Brückenkurzschluss oder „heißer Zweig“. Da Mosfets nicht unendlich schnell schalten können muss zwischen den Aktivierungen der Mosfets eine Totzeit eingefügt werden. In diesem Schaltzustand sind beide Mosfets deaktiviert. In unserer Schaltung kann die Totzeit über das Potentiometer RV4 eingestellt werden.
NE555
Der integrierte Baustein NE555 ist ein Urgestein der Elektrotechnik. Wann immer eine einfache Timerlösung benötigt wird um z.B. eine LED blinken zu lassen kommt der Baustein schon seit Jahrzehnten zum Einsatz. Die Eigenschaften dieses Schaltvorgangs wird über dessen äußere Beschaltung vorgegeben. Mithilfe von Widerständen und einem Kondensator kann der NE555 ein periodisch wiederholtes Schaltsignal erzeugen. Dies eignet sich perfekt zum ansteuern der MOSFET bzw. des Gatetreibers.
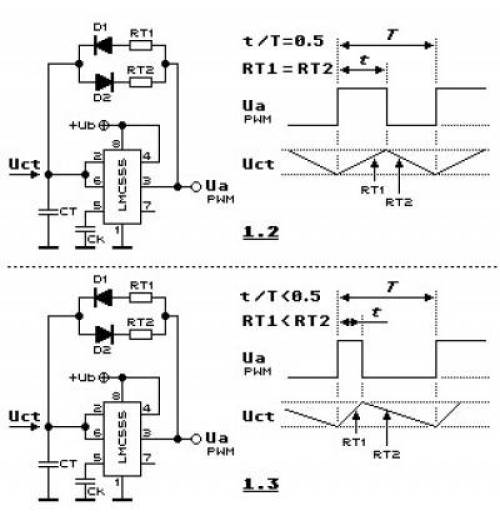
Über das Widerstandsverhältnis in obiger Schaltung kann der Duty-Cycle am Ausgang des Timers eingestellt werden.
Arduino Nano
Im Arduino Nano Every1) ist der ATMega 4809 verbaut. Ziel ist es ein frei einstellbares PWM-Signal zu erzeugen. Die Einstellung erfolgt über das Auslesen von zwei Potentiometern. Das PWM-Signal wird mit einem 16-Bit Timer bzw. Zähler erzeugt. Dazu wird die „Single-Slope PWM Generation“ Funktion des Timers genutzt. Generell kann die Funktionsweise so erklärt werden:
Während einer Periode zählt der Zähler linear von einem Startwart zu einem Endwert. Dazu kann ein Vergleichswert frei eingestellt werden. Immer wenn der Zähler dem Vergleichswert entspricht, wechselt das Ausgangssignal von „High“ auf „Low“ oder umgekehrt. Die Periodendauer hängt von der Größe des Endwertes und dementsprechend von der Auflösung ab. Die Mindestgröße des Endwert beträgt 2 Bit und Maximal 16 Bit. Mit der folgenden Formel kann die Auflösung berechnet werden:
RPWM_SS = (log[PER + 1]) / (log[2])
Wobei PER (Period) für den Wert bzw. die Länge der Periodendauer steht. Die Frequenz des PWM Signals hängt von der Periodendauer, der Frequenz der peripheren Uhr fCLK_PER und dem Prescaler ab.
fPWM_SS = fCLK_PER / N * (PER + 1)
Weitere Details können dazu dem Datenblatt entnommen werden. datenblatt.pdf
Zur PWM-Einstellung und Anzeige der aktuellen Daten auf dem Display kann folgender Programmcode verwendet werden:
//Einbinden der Header Dateien
#include <Wire.h>
#include <Adafruit_GFX.h>
#include <Adafruit_SSD1306.h>
//Festlegen des Display Höhe und Breite
#define SCREEN_WIDTH 128 // OLED display width, in pixels
#define SCREEN_HEIGHT 64 // OLED display height, in pixels
//Festlegen der Verbindung
// Declaration for an SSD1306 display connected to I2C (SDA, SCL pins)
Adafruit_SSD1306 display(SCREEN_WIDTH, SCREEN_HEIGHT, &Wire, -1);
//Festlegen der Variablen und deren Startwerte
int poti_frq_count_new = 0;
int poti_frq_count_old = -10;
double poti_frq_val;
int poti_frq = A0; // Frequency Poti
int poti_duty_count_new = 0;
int poti_duty_count_old = -10;
double poti_duty_val;
int poti_duty = A1; // Duty-Cycle Poti
void setup() {
Serial.begin(115200);
if(!display.begin(SSD1306_SWITCHCAPVCC, 0x3C)) { // Address 0x3D for 128x64
Serial.println(F("SSD1306 allocation failed"));
for(;;);
pinMode(9, OUTPUT);
}
}
//Hauptschleife
void loop()
{
// Frequency Potentiometer
poti_frq_count_new = 1023 - analogRead(poti_frq); //Frequenz Potentiometer auslesen und normieren.
//Dutycycle Potentiometer auslesen
// Duty-Cycle Potentiometer
poti_duty_count_new =
constrain(analogRead(poti_duty),51,973); //Maximale Grenzen für das Duty festlegen
//Entprellen der Potentiometer. Werte werden erst upgedatet wenn die Wertänderung größer 5 ist.
// Decide whether update of timer registers is necessary --> minimum delta of five to previous ADC counter
if (poti_frq_count_new - poti_frq_count_old > 5 || poti_frq_count_new - poti_frq_count_old < -5 || poti_duty_count_new - poti_duty_count_old > 5 || poti_duty_count_new - poti_duty_count_old < -5) {
poti_frq_count_old = poti_frq_count_new;
poti_duty_count_old = poti_duty_count_new;
// https://forum.arduino.cc/t/nano-every-pwm-frequency/602016/3
//Festlegen der Form des Ausgangssignals
// Set PB0 as output (waveform output, pg. 204)
PORTB.DIRSET = PIN0_bm;
// Values from 0 to 400 for setting correct frequency
poti_frq_val = (double) poti_frq_count_new/1023 * 400;
// Duty Cycle value between 0 and 100
poti_duty_val = (double) poti_duty_count_new/1023 * 100;
// Frequency: F_pwm_ss = Fclk_per/(N(PER+1)) with prescaler N = 1 and Fclk_per = 16MHz
// --> F_pwm_ss1 = 20kHz: PER+1 = 800
// --> F_pwm_ss2 = 40kHz: PER+1 = 400
// Max resolution: Rpwm_ss = (log(PER+1))/(log(2))
TCA0.SINGLE.PER = 399 + (int)poti_frq_val;
// CMP sets the duty cycle of the PWM signal -> CT = CMP0 / PER
// DUTY CYCLE is approximately 50% when CMP0 is PER / 2
TCA0.SINGLE.CMP0 = (int) ((double)poti_duty_count_new/1023 * (399 + poti_frq_val));
// Counter starts at 0
//TCA0.SINGLE.CNT = 0x00;
// Configuring CTRLB register
// Compare 0 Enabled: Output WO0 (PB0) is enabled
// Single slope PWM mode is selected
TCA0.SINGLE.CTRLB = TCA_SINGLE_CMP0EN_bm | TCA_SINGLE_WGMODE_SINGLESLOPE_gc;
// Using system clock (no frequency division, the timer clock frequency is Fclk_per)
// Enable the timer peripheral
TCA0.SINGLE.CTRLA = TCA_SINGLE_CLKSEL_DIV1_gc | TCA_SINGLE_ENABLE_bm;
}
else {
}
delay(2000);
display.clearDisplay();
display.setTextColor(WHITE);
display.setTextSize(1);
display.setCursor(0,0);
display.print("Frequency: ");
display.setTextSize(2);
display.setCursor(0,10);
display.print(20+(400-poti_frq_val)/400*20);
display.print(" kHz");
display.setTextSize(1);
display.setCursor(0, 35);
display.print("Duty-Cycle: ");
display.setTextSize(2);
display.setCursor(0, 45);
display.print(poti_duty_val);
display.print(" %");
display.display();
}
Dazu sind noch folgende Einstellungen und Bibliotheken notwendig:
- In der Arduino IDE unter Tools - Registers emulation → None (ATMEGA4809)
- Bibliotheken: Adafruit BusIO, Adafruit GFX Library, Adafruit_SSD1306
- Board-Manager: Arduino Nano Every installieren
Der Fehler: avrdude: jtagmkII_initialize(): Cannot locate „flash“ and „boot“ memories in description
kann ignoriert werden.
Aufgabe 9
Jetzt geht es an die Inbetriebnahme der Schaltung. Organisieren Sie sich dazu im ersten Schritt eine Platine und alle benötigten Bauelemente.
Die Platine enthält auch einige SMD Bauteile. Falls Sie Hilfe benötigen beim Löten melden Sie sich bitte. Sie können den SMD-Lötplatz verwenden oder alternativ mit einer feinen Lötspitze arbeiten, siehe Einführungsvideo.
Lötanleitung (Interner Link, bitte anmelden)
Allgemeine Hinweise:
- Orientieren Sie sich am Labormuster
- Achten Sie auf die richtige Polarität gepolter Bauelemente
- Alle ICs, Arduino und das Display werden auf Sockel montiert
- Halten Sie sich an die nachfolgende Reihenfolge bei der Inbetriebnahme
- Die RC-Snubber (Dämpfungsschaltung parallel zu den Mosfets) bitte noch nicht mit auflöten
- Die Filterelemente noch nicht mit auflöten. Zur Funktion werden die Jumper über der Gleichtaktdrossel und der Filterspule benötigt!
- Nehmen Sie den Timerbaustein und den Mikrocontroller in Betrieb
- Überprüfen Sie ob die PWM-Muster richtig ausgegeben werden und bestimmen Sie die einstellbaren Duty-Cycle Bereich
- Erklären Sie warum der Duty-Cycle nicht von 0 … 100% eingestellt werden kann (das ist so gewollt und kein Fehler)
- Löten Sie nun den Treiberbaustein auf und überprüfen Sie ob die Ansteuersignale für den Low-Side Mosfet richtig ausgegeben werden
- Welches Signal erwarten Sie für die Ansteuerung des High-Side Mosfet? Messen Sie das Signal, worauf ist dabei zu achten?
- Installieren Sie die restlichen Bauelemente und überprüfen Sie ob die Schaltung funktioniert.
- Überlegen Sie sich Kriterien wie Sie die Funktion der Schaltung mit den vorhandenen Messgeräten überprüfen können
Achtung: Lötzinn ob bleihaltig oder nicht ist enthält giftige Chemikalien. Bitte waschen Sie sich nach Ihrer Arbeit sorgfältig die Hände.
Teil4: Messung und Entstörung
Bei der Entwicklung unserer Sitzheizung müssen wir natürlich alle Verkaufsoptionen bei den EMV-Messungen berücksichtigen, also die Basis- und die Premiumvariante. B EMV-Messungen, zumindestens die Emissionsmessungen, haben prinzipiell immer einen ähnlichen Verlauf.
Allgemeiner Messablauf
Bevor es losgeht mit den Messungen müssen einige Vorarbeiten erledigt werden. Von vielen Kunden verlangt ist ein sogenannter EMV-Prüfplan.
Der EMV-Prüflan enthält folgende Punkte
- Einfache Funktionsbeschreibung
- Blockschaltbild des Prüflings
- Skizze zum Messaufbau mit Hilfsmittel
- Einzuhaltende Grenzwerte
- Betriebszustände während der Messung
Nach einer erfolgten Messung werden die Ergebnisse in den Prüfplan mit eingefügt und man erhält den EMV-Prüfbericht.
Schritt 1: Verifikation Messgerät
Diesen Schritt haben wir bereits beim Kennenlernen der Messgeräte durchgeführt. Wichtige Messgeräte müssen nicht nur regelmäßig kalibriert werden, sondern eigentlich vor jeder Messung auf die korrekte Arbeitsweise überprüft werden. Stellen Sie sich vor Sie bereiten eine Abnahmemessung vor und durch einen Bedienfehler zeigt ein Messgerät zur geringe Ergebnisse an. Werden daraufhin tausende von Einheiten produziert und eine EMV-Problem wird erst spät erkannt - zum Beispiel weil ein Kommunikationsverbindung eines selten genutzten Dienstes ausfällt - hat Ihre Firma ein Problem!
Schritt 2: Verifikation Systemaufbau
Im nächsten Schritt überprüfen wir ob sich Störungen von außen in unseren Messaufbau einschleichen. EMV-Messungen werden normalerweise in geschirmten Kabinen (EMV-Kabine oder Absorberhalle, engl. anechoic chamber) durchgeführt, mit dem Ziel, dass keine Störungen nach außen treten können - bei Störfestigkeitsprüfungen - oder in unserem Fall für die Emissionsmessung keine Störungen von außen eindringen können und das Messergebnis verfälschen. Nicht nur von außen eindringende Signale sind ein Problem. Auch notwendige Messtechnik (z.B. CAN-Messtechnik) oder Hilfsspannungsquellen können Störungen generieren die nicht vom Prüfling selber kommen. Im schlimmsten Fall erzeugt sich das Messgerät intern selber die Störungen welche dauerhaft im Spektrum sichtbar sind. Um hier alle Fehler auszuschließen und um sicherzustellen, dass die gemessenen Störungen auch von unserem Prüfling kommen machen wir eine Leermessung oder auch Rauschmessung. Dazu stellen wir das Messgerät entsprechend den Anforderungen der Norm im betrachteten Frequenzbereich und Bandbreite ein und führen eine Messung durch. Wichtig ist, dass dabei alle Leitungsverbindungen, Spannungsversorgung usw. aktiv bzw. vorhanden sind, der Prüfling bleibt allerdings inaktiv (Hauptschalter unterbrochen bzw. Spannungsversorgung abgezogen in unserem Fall).
Schritt 3: Bestandsaufnahme
Jetzt geht es darum ein Gefühl dafür zu bekommen ob das Gerät eventuell bereits die Grenzwerte einhält oder ob wir durch Hardwaremaßnahmen nachbessern müssen. Während der Bestandsaufnahme wird der Prüfling in definierte Zustände gebracht (typische Anwendungsfälle), die Emissionen gemessen und gegenüber den Grenzwertlinien bewertet. Bei einer Kundenentwicklung werden die Betriebszustände und der Messaufbau mit dem Auftraggeber abgesprochen. Bei Plattformentwicklungen, also Vorausentwicklungen eines Zulieferers können Sie die Zustände selber sinnvoll festlegen.
Schritt 4: Entstörung
Die ersten drei Schritte sind üblicherweise langweilig und laufen routiniert in vielen EMV-Laboren bzw. EMV-Abteilungen ab. Spannend wird es wenn die Grenzwerte überschritten sind und wir uns auf die Suche machen müssen nach geeigneten Gegenmaßnahmen. Zur Reduktion leitungsgebundener Emissionen kommen üblicherweise Filter in den Versorgungsleitungen zum Einsatz. In unserem EMV-Versuch haben wir es einfach, und müssen lediglich die Jumper über den Filterelementen entfernen. In der Realität gilt es geeignete Filterlemente auszuwählen entsprechend dem Bauraum und der geforderten Stromtragfähigkeit, Spannungsfestigkeit, usw.. Besonders bei der Auswahl geeigneter Filterelemente haben wir die Möglichkeit die Störungen in Gleich- und Gegentaktstörungen zu zerlegen und so die Filter gezielt im entsprechenden Frequenzbereich auszulegen.
Falls das alles nichts hilft oder zu wenig Bauraum vorhanden ist muss die Schaltung optimiert werden. In detektivischer Arbeit gilt es dann herauszufinden welche Baugruppe für die Störungen verantwortlich ist um diese dann lokal zu bekämpfen bzw. das Layout ggf. zu optimieren.
Hinweis: Wir betrachten für unseren Aufbau nur die Maximalwerte der Störungen. Das bedeutet wir messen stets mit einem Spitzenwertdetektor. Durch die hohe Taktfrequenz des Tiefsetzstellers haben die verschiedenen Messverfahren Spitzenwert- Mittelwert- und Quasispitzenwert nahezu identische Ergebnisse. Bewertet werden müssen stets die Störungen für beide Versorgungsklemmen (Bat + und Bat -).
Die Schritte 1 - 3 werden üblicherweise im Prüfplan und Prüfbericht mit dokumentiert und deuten damit auf ein vertrauenswürdiges Ergebnis hin. Finale EMV-Prüfberichte werden nur mit eingehaltenen Grenzwerte veröffentlicht oder nach außen bzw. an den Kunden gegeben. Bei eingefügten Entstörmaßnahmen oder optimierten Schaltungen bzw. Layouts handelt es sich um technisches Know-How Ihrer Firma und Ihnen und wird entsprechend vertraulich behandelt!
Aufgabe 10
- Erstellen Sie für die Komponente Sitzheizung einen EMV-Prüfplan
- Führen Sie die Schritte 1 - 3 der Messung durch und bewerten Sie die Ergebnisse. Vergleichen Sie dazu die Messergebnisse mit den geforderten Grenzwerten
- Führen Sie als Vorbereitung der Filterauslegung eine Gleich- Gegentaktanalyse durch und bestimmen Sie die dominante Störgrößen. Verwende Sie dazu die Power-Splitter (ZFSC-2-4+ zur Ermittlung der Gleichtaktstörungen, ZFSCJ-2-1+ zur Ermittlung der Gegentaktstörungen), siehe EMV-Skript
Entstörung
In unserem Beispiel gilt es die Grenzwerte der leitungsgebundenen Emissionen einzuhalten. Da in modernen Fahrzeugen, und dabei vor allem im Innenraum, sehr viel Elektronikkomponenten
verbaut sind, müssen wir davon ausgehen, dass unsere Kunden die schärfsten Grenzwerte an unsere Komponente anlegen. Das bedeutet, wir müssen die Komponente entstören. Bisher haben wir den Eingangsfilter außen vorgelassen und ohne
jegliche Filterschaltung in den Versorgungsleitungen gemessen. In der Realität kommt keine Komponente ohne solche Filter am Eingang aus, womit diese immer im Design berücksichtigt werden müssen. Die Kunst besteht nun darin
die Filterschaltung so klein wie notwendig und natürlich auch so günstig wie möglich darzustellen. Daher ist es immer schlauer die Entstehung hochfrequenter Emissionen zu verhindern, also die Störquelle zu reduzieren, als später deren
Auswirkungen zu unterdrücken.
Die wichtigsten Layoutregeln lauten hier:
- Masse stets so niederohmig wie möglich gestalten
- Rückstrompfade nicht dem Zufall überlassen und dafür sorgen, dass diese nahe der Zuleitung verlaufen können
- Strompfade bzw. Schleifen so klein wie möglich halten
Während der Entwicklung der Platine in einem studentischen Projekt wurden einige Punkte bereits berücksichtigt. Da die Grenzwerte noch nicht ganz eingehalten werden können müssen wir nun eine geeignete Filterschaltung wählen.
Nachfolgende Abbildung zeigt die möglichen Filterschaltungen die auf der Platine umgesetzt werden können:
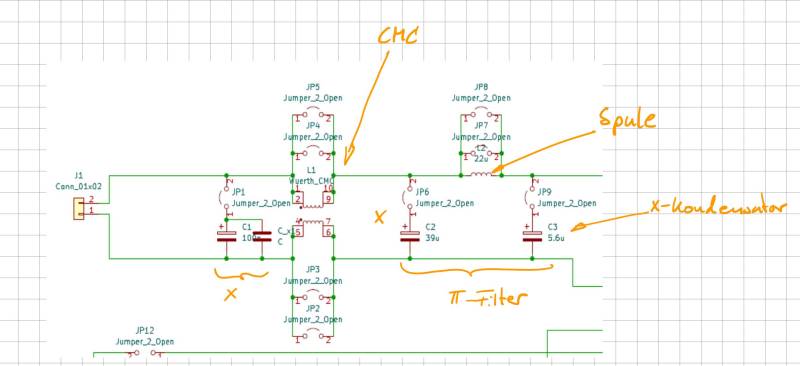
Die Gleichtaktspule und die Filterinduktivität sind fest vorgegeben. Die Bauteile der Kondensatoren können Sie nach belieben wählen. Es muss lediglich der Footprint auf der Platine mit Ihrer Auswahl übereinstimmen. Die im Schaltplan angegebenen Werte sind Richtwerte und müssen nicht übernommen werden. In einem realen Projekt wäre die Schaltung vorgegeben und Sie als EMV- Ingenieur müssen nun mit dem vorhandenen Filerdesign das Beste Ergebnis erzielen.
Schauen Sie sich doch einfach mal die Datenblätter der Gleichtaktspule L1 744290121-1721527.pdf und der Filterinduktivität L2 7447709220.pdfim Datenblatt an.
Dabei sind vor allem die Impedanzverläufe über der Frequenz interessant. Eine Spule soll ja hochfrequenten Strömen blockieren. Das bedeutet natürlich je höher die Impedanz, desto besser für uns. Auffällig ist natürlich jeweils, dass die Impedanz oberhalb
der Resonanzfrequenz drastisch abfällt.
Impedanzanalysator
Die verfügbaren Kondensatoren (X-Kondensatoren) können wir selber nachmessen mit unserem Impedanzanalysator.
Der Impedanzanalysator dient dazu die Impedanz und die Phasenverschiebung eines beliebigen Bauteils zu ermitteln. In diesem Fall sind mit dem Gerät die Verläufe von 20Hz bis 120MHz darstellbar. Die folgende Einweisung soll helfen den Impedanzanalysator bis zur Betriebsfähigkeit einzustellen.
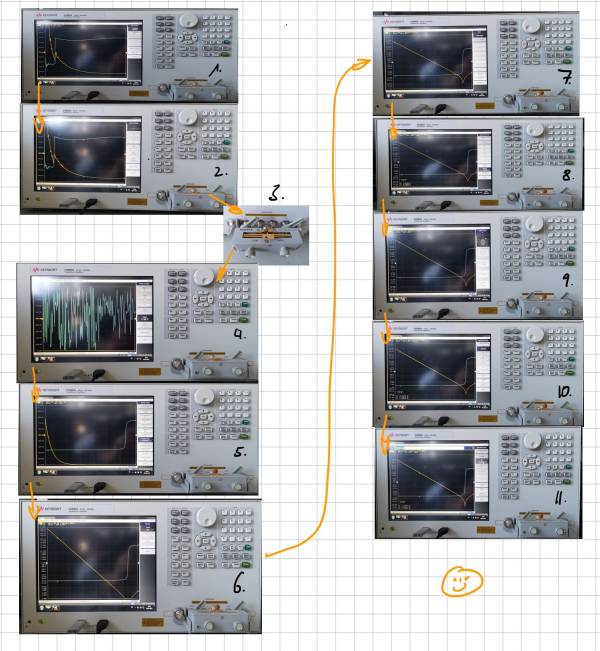
- Nach dem Hochfahren zeigt der Impedanzanalysator die Impedanz und die Phasenverschiebung in einem bestimmten Frequenzbereich an. Nun muss die verwendete Messeinrichtung kalibriert werden. Dazu wird zuerst mit der Taste „Cal“ das Kalibrierungsmenü geöffnet. Daraufhin muss mit dem Menüpunkt „Accessory“ die verwendete Messeinrichtung ausgewählt werden.
- In diesem Beispiel wurde der Messadapter „16047E“ verwendet. In dem Untermenü „Fixture Compen“ wird die Kalibrierung gestartet. Zuerst wird der Messadapter „offen“ kalibriert. Dabei darf kein Bauteil eingespannt sein. Mit dem Button „open“ wird die Kalibrierung gestartet. Mit einem Piepsen ist der Vorgang abgeschlossen.
- Für den nächsten Schritt wird ein definiertes Bauteil in den Adapter eingespannt (Kurzschlussbügel). Dieses „goldene Plättchen“ ist mit an gerändelten Schraube an dem Messadapter befestigt. Das Plättchen ist zu lösen und in den Messadapter einzuspannen.
- Als nächstes wird im gleichen „Fixture Compen“ Menü die Kalibrierungsoption „Short“ genutzt. Wieder wird mit einem Piepsen den Abschluss des Vorgang bestätigt. Damit ist die Kalibrierung des Messadapter abgeschlossen. Nun können die Bauteile vermessen werden. Das weitere Vorgehen wird Anhand von einem 10nF Keramikkondensator beschrieben. Zuerst wird das Bauteil in den Messadapter eingespannt.
- Nun sollte Anzeige eingestellt werden. Dies erfolgt im „Sweep Setup“ Menü. Mit der Einstellung „Sweep Type“ und dann auf „Log Freq“ wird der Frequenzbereich logarithmisch dargestellt.
- Im „Format“ Menü kann zusätzlich sie Y-Achsen Skalierung auf logarithmisch eingestellt werden.
- Um nun die Anzeigen hinreichend passend darzustellen, kann im Menü „Scale“ die Funktion „Auto Scale“ für eine Darstellung bzw. „Auto Scale All“ für alle Darstellungen verwendet werden.
- Die Auswertung der Ergebnisse erfolgt im „Analysis“ Menü. Um nun die Werte von der Kapazität, der Induktivität und des Widerstandes zu ermitteln, muss das Untermenü „Equivalent Circut“ ausgewählt werden. Der Sinn dieses Menü ist es die realen Werte des Bauteils mit denen von einer bestimmten Ersatzschaltung zu vergleichen. Wenn die Verläufe der Ersatzschaltung mit denen des realen Bauteils übereinstimmen, sind die Werte des Bauteils gefunden. Um den Visuellen Vergleich zu starten, sollten die Einstellungen „Simulate“ und „Display“ auf „ON“ gestellt werden.
- Nun muss eine Ersatzschaltung für das Bauteil im Untermenü „Select Circut“ ausgewählt werden. Die Wahl der Ersatzschaltung hängt von der Art des Bauteils ab.
- Man sollte verschiedene Ersatzschaltungen verwenden und dann über die Plausibilität der berechneten Werte nachdenken. Um einen berühmten Professor zu zitieren:„ Wenn die Bauteilwerte negativ sind, ist das schonmal schlecht“. Mit der Wahl des Ersatzschaltbild, kann nun im „Equivalent Circut“ Menü der Button „Calculate“ verwendet werden.
- Jetzt versucht das Programm Bauteilwerte zu bestimmen, welche einen Verlauf der Ergebnisse ergeben, die den realen Verläufen möglichst nahe kommen. Bei einfachen Bauteilen, wie diesem Kondensator, ist dies sehr zuverlässig. Wenn die Verläufe übereinstimmen, sind die Bauteilwerte bestimmt. Bei komplexeren Bauteilen kann es vorkommen, dass die Verläufe nicht sofort übereinstimmen. Dann können die Bauteilwerte der Ersatzschaltung angewählt und mit dem Stellrad oder mit den Nummerntasten nachkorrigiert werden.
Aufgabe 11
Bei der Auswahl der Filterelemente geht man üblicherweise wie folgt vor:
Schritt 1:
Bestimmen der dominierenden Störgröße (Gleich- oder Gegentaktstörung). Diese Aufgabe haben wir bereits erledigt. Wir kennen nun die Größe gegen die wir hauptsächlich etwas unternehmen müssen. Typischerweise sind Gegentaktstörungen für tiefe Frequenzen dominant, Gleichtaktstörungen für Frequenzen ab ca. 10 MHz. Der Übergang zwischen den dominanten Störgrößen hängt hauptsächlich vom Aufbau ab, wobei es keinen allgemeine Regel gibt in welchem Frquenzbereich eine Störgröße dominiert.
Schritt 2:
Mit dem Wissen über die dominante Störgröße suchen wir uns nun ein geeignetes Filterelement aus und überprüfen in einer erneuten Messung die Wirkung. Da die Grenzwerte stets auf „nodale“ Größen, also gegen Referenzmasse bezogen sind müssen wir nun noch überprüfen ob durch das
Filterelement auch eine Wirkung gegenüber den Grenzwerten erzielt werden kann.
Bei der Bewertung der Filterelemente stellen wir stets Messungen gegenüber mit / ohne Filterelement sowohl für Gleich-/ Gegentaktwirkung, als auch für die nodalen Größen.
Schritt 3:
Wir wiederholen die Schritte mit verschiedenen Filterelementen bis wir die Grenzwerte einhalten oder uns die Ideen ausgehen
Sollte das der Fall sein bleibt nur noch die Möglichkeit die Filterstruktur zu ändern (also alles von Vorne) oder nach der Quelle der Störungen zu suchen. Ist die Störquelle bekannt ist es vielleicht möglich durch eine Layoutänderung die EMV-Eigenschaften zu verbessern oder lokale
Filter einzufügen. In vielen Fällen kann ein weiteres Hardwaremuster jetzt nicht mehr abgewendet werden. Für den Projektzeitplan hat dies ggf. fatale Folgen.
Glück des Tüchtigen:
Auch Lösungen die auf den ersten Blick nichts mit den Versorgungsleitungen zu tun haben können helfen.
Probieren Sie es doch einfach aus:
- Filter im Ausgangspfad (an der Last)
- Ferrite auf der Zuleitung (können zur Not auch noch spät im Projekt angebracht werden)
- Ferrit im Ausgangspfad (Heizelement)
Fazit:
EMV-Optimierungen in einer späten Musterphase (C-Muster bzw. Vorserie) sind viel zu spät. Treten Grenzwertüberscheitungen auf die durch reine Bauteilanpassungen nicht mehr behebbar sind muss ein neuer Musterstand eingeplant werden.
- Messen Sie den Betrag der Impedanz verschiedener Kondensatoren und überlegen Sie ob diese als X-Kondensatorelement zum Einsatz kommen können. Stellen Sie den Impedanzverlauf verschiedener Kondensatoren gegenüber.
- Suchen Sie nach der besten Filterlösung für unser Produkt
- Erklären Sie warum in unserem Beispiel keine Y-Kondensatoren zum Einsatz kommen können.
- Erstellen Sie einen EMV-Prüfbericht mit dem Fazit und Endergebnis
Hinweis: Die von uns hier entwickelte Sitzheizung reicht nur für einen kleinen Sitz. Die Sitzheizung in modernen Fahrzeugen hat eine Leistung von mehreren hundert Watt.